题目内容
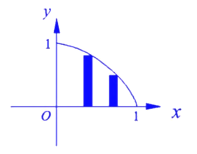
【题目】在平面直角坐标系中,函数![]() 在第一象限内的图像如图所示,试做如下操作:把x轴上的区间
在第一象限内的图像如图所示,试做如下操作:把x轴上的区间![]() 等分成n个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数
等分成n个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数![]() 的图像上.若用
的图像上.若用![]() 表示第k个矩形的面积,
表示第k个矩形的面积,![]() 表示这n个叫矩形的面积总和.
表示这n个叫矩形的面积总和.
(1)求![]() 的表达式;
的表达式;
(2)利用数学归纳法证明![]() ,并求出
,并求出![]() 的表达式
的表达式
(3)求![]() 的值,并说明
的值,并说明![]() 的几何意义.
的几何意义.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]() ;(3)
;(3)![]() .
.![]() 的几何意义表示函数
的几何意义表示函数![]() 的图象与
的图象与![]() 轴,及直线
轴,及直线![]() 和
和![]() 所围曲线梯形的面积.
所围曲线梯形的面积.
【解析】
(1)第![]() 个矩形的高为
个矩形的高为![]() ,面积易得;
,面积易得;
(2)用数学归纳法证明;由此等式可求得![]() .
.
(3)根据极限的性质求极限.
(1)由题意第![]() 个矩形的高是
个矩形的高是![]() ,∴
,∴![]() ;
;
(2)(i)![]() 时,
时,![]() ,命题成立,
,命题成立,
(ii)设![]() 时命题成立,即
时命题成立,即![]() ,
,
则![]() 时,
时,![]()
![]()
![]() ,
,
∴![]() 时命题成立,
时命题成立,
综上,![]() 时,命题为真,即
时,命题为真,即![]() ,
,

![]() ;
;
(3)![]() .
.
![]() 的几何意义表示函数
的几何意义表示函数![]() 的图象与
的图象与![]() 轴,及直线
轴,及直线![]() 和
和![]() 所围曲线梯形的面积.
所围曲线梯形的面积.

练习册系列答案
相关题目
【题目】在信息时代的今天,随着手机的发展,“微信”越来越成为人们交流的一种方法,某机构对“使用微信交流”的态度进行调查,随机抽取了100人,他们年龄的频数分布及对“使用微信交流”赞成的人数如下表:(注:年龄单位:岁)
年龄 |
|
|
|
|
|
|
频数 | 10 | 30 | 30 | 20 | 5 | 5 |
赞成人数 | 9 | 25 | 24 | 9 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的![]() 列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() ,
,![]() 调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.