题目内容
已知f(x)＝3sin x－πx，命题p：∀x∈
，f(x)＜0，则( )
A．p是真命题，綈p：∀x∈，f(x)＞0
B．p是真命题，綈p：∃x0∈，f(x0)≥0
C．p是假命题，綈p：∀x∈，f(x)≥0
D．p是假命题，綈p：∃x0∈，f(x0)≥0
B 命题立意：本题主要考查函数的性质与命题的否定的意义等基础知识，意在考查考生的运算求解能力．
解题思路：依题意得，当x∈时，f′(x)＝3cos x－π＜3－π＜0，函数f(x)是减函数，此时f(x)＜f(0)＝3sin 0－π×0＝0，即有f(x)＜0恒成立，因此命题p是真命题，綈p应是“∃x0∈，f(x0)≥0”．故选B.
练习册系列答案
相关题目
下图是7位评委给某作品打出的分数的茎叶图，那么这组数据的方差是________．
| 8 | 8 | 9 | 9 | |
| 9 | 0 | 1 | 1 | 2 |
－
－x在R上为减函数；p2：函数y＝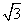
的正三角形，且圆与三角形内切，则侧(左)视图的面积为( )
