题目内容
1.已知$\overrightarrow{u}$=(x,y)与向量$\overrightarrow{v}$=(y,2y-x)的对应关系用$\overrightarrow{v}$=f($\overrightarrow{u}$)表示.(1)证明:对于任意向量$\overrightarrow{a}$,$\overrightarrow{b}$及常数m、n,恒有f(m$\overrightarrow{a}$+n$\overrightarrow{b}$)=mf($\overrightarrow{a}$)+nf($\overrightarrow{b}$)成立.
(2)设$\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(1,0),求向量f($\overrightarrow{a}$)及f($\overrightarrow{b}$)的坐标.
(3)求使f($\overrightarrow{c}$)=(3,5)成立的向量$\overrightarrow{c}$.
分析 (1)设出任意向量的坐标$\overrightarrow{a}$,$\overrightarrow{b}$分别计算要证等式的左边的右边,比较计算结果可得等式成立
(2)直接利用题中的对应关系求出 f($\overrightarrow{a}$)=(1,2-1)=(1,1),f($\overrightarrow{b}$)=(0,2×0-1)=(0,-1),
(3)设$\overrightarrow{a}$=(x,y),则 f($\overrightarrow{a}$)=(y,2y-x)得到方程组,解得即可.
解答 (1)设$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),
∴m$\overrightarrow{a}$+n$\overrightarrow{b}$=(mx1+nx2,my1+ny2 ),
∴f(m$\overrightarrow{a}$+n$\overrightarrow{b}$)=(my1+ny2,2my1+2ny2-mx1-nx2 ),
∴mf($\overrightarrow{a}$)+nf($\overrightarrow{b}$)=m(y1,2y1-x1 )+n(y2,2y2-x2 )=( my1+ny2,2my1+2ny2-mx1-nx2 ),
∴对于任意向量$\overrightarrow{a}$,$\overrightarrow{b}$及常数m、n,恒有f(m$\overrightarrow{a}$+n$\overrightarrow{b}$)=mf($\overrightarrow{a}$)+nf($\overrightarrow{b}$)成立,
(2)f($\overrightarrow{a}$)=(1,2-1)=(1,1),f($\overrightarrow{b}$)=(0,2×0-1)=(0,-1),
(3)设$\overrightarrow{a}$=(x,y),则 f($\overrightarrow{a}$)=(y,2y-x),∴$\left\{\begin{array}{l}{y=3}\\{2y-x=5}\end{array}\right.$,
∴x=1,y=3,∴$\overrightarrow{c}$(1,3).
点评 本题考查两个向量坐标形式的运算,以及用待定系数法求向量的坐标.

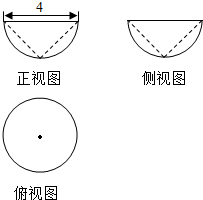 如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为( )
如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为( )| A. | 3:1 | B. | 2:1 | C. | 1:1 | D. | 1:2 |
| A. | 0<n<m | B. | n<m<0 | C. | 0<m<n | D. | m<n<0 |
 令y=f(x),给出一个语句如图所示,根据语句,可求得
令y=f(x),给出一个语句如图所示,根据语句,可求得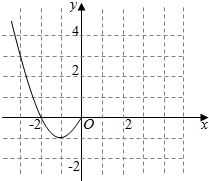 已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象:
已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象: