题目内容
10.己知点P的极坐标为(2,$\frac{π}{4}$),直线l过点P且与极轴所成的角为$\frac{π}{3}$,求直线l的极坐标方程.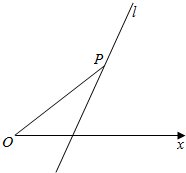
分析 点P的极坐标为(2,$\frac{π}{4}$),化为直角坐标P$(\sqrt{2},\sqrt{2})$.由于直线l过点P且与极轴所成的角为$\frac{π}{3}$,利用点斜式可得点斜式,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入即可得出.
解答 解:点P的极坐标为(2,$\frac{π}{4}$),化为直角坐标P$(\sqrt{2},\sqrt{2})$.
∵直线l过点P且与极轴所成的角为$\frac{π}{3}$,
∴y-$\sqrt{2}$=$(x-\sqrt{2})$$tan\frac{π}{3}$,
即y-$\sqrt{2}$=$\sqrt{3}$$(x-\sqrt{2})$,
把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入可得:$\sqrt{3}ρcosθ$-ρsinθ+$\sqrt{2}$-$\sqrt{6}$=0.
∴直线l的极坐标方程为$\sqrt{3}ρcosθ$-ρsinθ+$\sqrt{2}$-$\sqrt{6}$=0.
点评 本题考查了极坐标化为直角坐标、点斜式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
20.设全集U={1,2,3,4,5},集合A={1,2,4},B={4,5},则集合A∩(∁UB)=( )
| A. | {1,2} | B. | {3,5} | C. | {4} | D. | {5} |
