Question

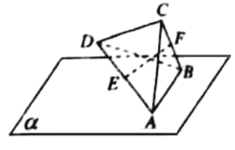
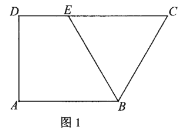
【题目】图1是直角梯形，，，，，，.以为折痕将折起，使点到达的位置，且，如图2.

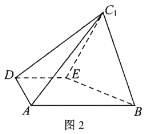
（1）证明：平面平面；

（2）求直线与平面所成角的正弦值.

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）做辅助线，先根据线线垂直证明面，进而可证平面平面；

（2）建立平面直角坐标系，求出平面的法向量，利用法向量法可求直线与平面所成角的正弦值.

（1）证明：在图1中，连结，由已知得

∵且，

∴四边形为菱形，

连结交于点，

∴，

又∵在中，，

∴，

在图2中，，

∵，∴，

由题意知，

∴span>面，又平面，

∴平面平面；

（2）如图，以为坐标原点，，分别为轴，方向为轴正方向建立空间直角坐标系.由已知得各点坐标为

，

所以，，，

设平面的法向量为，则，

所以，即，令，解得，

所以，

所以，

记直线与平面所成角为，

则.