题目内容
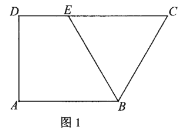
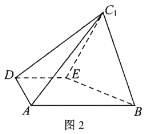
【题目】在四面体![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,现将四面体以
的中点,现将四面体以![]() 为轴旋转,则线段
为轴旋转,则线段![]() 在平面内投影长度的取值范围是__________.
在平面内投影长度的取值范围是__________.
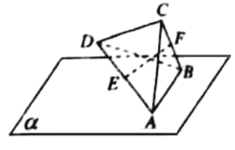
【答案】![]()
【解析】
取![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,利用三角形的中位线得
,利用三角形的中位线得![]() ,
,![]() ,根据等腰三角形的性质和线面垂直的判定定理,可证出
,根据等腰三角形的性质和线面垂直的判定定理,可证出![]() 平面
平面![]() ,进而得出
,进而得出![]() ,
,![]() ,当四面体绕
,当四面体绕![]() 旋转时,
旋转时,![]() 与
与![]() 的垂直性保持不变,当
的垂直性保持不变,当![]() 与平面
与平面![]() 垂直时,
垂直时,![]() 在平面
在平面![]() 上的射影
上的射影![]() 的长取得最小值,当
的长取得最小值,当![]() 与平面
与平面![]() 平行时,
平行时,![]() 在平面
在平面![]() 上的射影
上的射影![]() 的长取得最大值,由此即可得出结果.
的长取得最大值,由此即可得出结果.
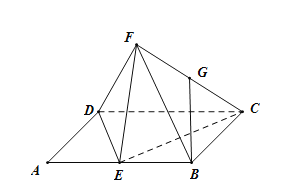
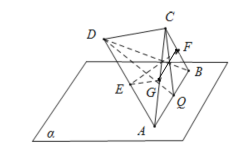
解:如图,取![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() 分别是线段
分别是线段![]() 和
和![]() 的中点,
的中点,
![]() ,
,![]() ,
,
由于![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
当四面体绕![]() 旋转时,
旋转时,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 与
与![]() 的垂直性保持不变,且
的垂直性保持不变,且![]() ,长度不变,
,长度不变,
当![]() 与平面
与平面![]() 垂直时,
垂直时,![]() 在平面上的射影长最短为0,
在平面上的射影长最短为0,
此时![]() 在平面
在平面![]() 上的射影
上的射影![]() 的长取得最小值为
的长取得最小值为![]() ,
,
当![]() 与平面
与平面![]() 平行时,
平行时,![]() 在平面上的射影长最长为:
在平面上的射影长最长为:![]() ,
,
此时![]() 在平面
在平面![]() 上的射影
上的射影![]() 的长取得最大值为
的长取得最大值为![]() ,
,
![]() 线段
线段![]() 在平面
在平面![]() 上的射影长的取值范围是
上的射影长的取值范围是![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】随着社会经济高速发展,人民的生活水平越来越高,部分学校安装了中央空调,某校数学建模队调查了某品牌中央空调,得到该设备使用年限x(单位:年)和维修总费用y(单位:万元)的统计表如下:(每年年底维修保养)
使用年限x(单位:年) | 2 | 3 | 4 | 5 | 6 |
维修总费用y(单位:万元) | 1 |
| 3 | 4 |
|
由上表可得线性回归方程![]() ,则根据此模型预报该品牌中央空调第8年年底的维修费用约为( )
,则根据此模型预报该品牌中央空调第8年年底的维修费用约为( )
A.![]() 万元B.
万元B.![]() 万元C.
万元C.![]() 万元D.
万元D.![]() 万元
万元