题目内容
椭圆
=1的右焦点为F，定点A（1,
），点M在椭圆上，当|AM|+2|MF|为最小值时，求点M的坐标．
思路分析：本题的关键是求出离心率e=，把2|MF|转化为M到右准线的距离，从而得最小值．一般地，求|AM|+
|MF|均可用此法．
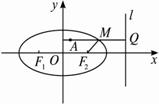
解：如图，由已知：a=4,c=2．所以e=
，右准线l:x=8．
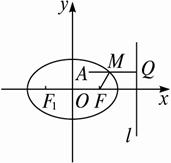
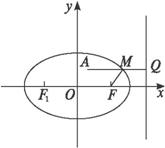
过A作AQ⊥l，垂足为Q，交椭圆于M，故|MQ|=2|MF|．显然|AM|+2|MF|的最小值为|AQ|，即M为所求点，因此ym=
，且M在椭圆上．故xm=
．所以M（
,
）．
方法归纳 本题关键在于未知式|AM|+2|MF|中的“2”的处理．事实上，如图，e=
，即|MF|是M到右准线的距离的一半，即图中的MQ，问题转化为求椭圆上一点M，使M到A的距离与到右准线距离之和取最小值．
练习册系列答案
阅读快车系列答案
相关题目
+
=1的右焦点为F,过点A(1,3),点M在椭圆上,当|AM|+2|MF|为最小值时,求点M的坐标.
|MF|均可用此法.?
），椭圆
=1的右焦点为F，点P在椭圆上移动.当|PA|+2|PF|取最小值时,P点的坐标是_________.
+
=1的右焦点为F，已知点A（1,
），点M在椭圆上，当|AM|+2|MF|为最小值时，求点M的坐标. 
=1的右焦点为F,设A(-
,3),P是椭圆上一动点,则|AP|+5|PF|取最小值时,P的坐标为( )
)，椭圆
+ 
=1的右焦点为F，点P在椭圆上移动.当|PA|+2|PF|取最小值时,P点的坐标是多少？