题目内容
已知函数f(x)=2sinxsin(
-x)+
sinxcosx+cos2x
(1)求函数f(x)的最小正周期和单调递增区间;
(2)若0≤x≤
,求函数f(x)的最值及取得最值时相应x的值.
| π |
| 3 |
| 3 |
(1)求函数f(x)的最小正周期和单调递增区间;
(2)若0≤x≤
| π |
| 2 |
考点:两角和与差的正弦函数,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)利用三角恒等变换对y=f(x)化简可得f(x)=2sin(2x+
),利用正弦函数的周期性与单调性即可求得函数f(x)的最小正周期和单调递增区间;
(2)0≤x≤
⇒
≤2x+
≤
,利用正弦函数的单调性与闭区间上的最值即可求得答案.
| π |
| 6 |
(2)0≤x≤
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
解答:
解:(1)f(x)=2sinxsin(
-x)+
sinxcosx+cos2x
=2sinx(
cosx-
sinx)+
sin2x+cos2x
=
sin2x+cos2x
=2sin(2x+
)…3分
T=
=π…4分
2kπ-
≤2x+
≤2kπ+
,k∈Z
-
+kπ≤x≤
+kπ,k∈Z,
故函数f(x)的单调递增区间为[-
+kπ,
+kπ],k∈Z;…7分
(2)因为0≤x≤
,得
≤2x+
≤
,…8分
2x+
=
,即x=
时,f(x)max=2;
2x+
=
,即x=
时,f(x)min=-1;
所以,x=
时,f(x)max=2;x=
时,f(x)min=-1…12分
| π |
| 3 |
| 3 |
=2sinx(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=
| 3 |
=2sin(2x+
| π |
| 6 |
T=
| 2π |
| 2 |
2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
-
| π |
| 3 |
| π |
| 6 |
故函数f(x)的单调递增区间为[-
| π |
| 3 |
| π |
| 6 |
(2)因为0≤x≤
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
2x+
| π |
| 6 |
| 7π |
| 6 |
| π |
| 2 |
所以,x=
| π |
| 6 |
| π |
| 2 |
点评:本题考查三角恒等变换的应用,考查正弦函数的单调性、周期性与闭区间上的最值,考查转化思想与运算能力,属于中档题.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
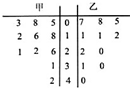 某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们在这11场比赛的得分用下面的茎叶图表示,设甲运动员得分的中位数为M1,乙运动员得分的中位数为M2,则在下列选项中,正确的是( )
某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们在这11场比赛的得分用下面的茎叶图表示,设甲运动员得分的中位数为M1,乙运动员得分的中位数为M2,则在下列选项中,正确的是( )| A、M1=18,M2=11 |
| B、M1=81,M2=12 |
| C、M1=8,M2=2 |
| D、M1=3,M2=1 |
圆x2+y2+2x-4y=0的半径为( )
| A、3 | ||
B、
| ||
C、
| ||
| D、5 |