题目内容
已知P(2,0),Q(8,0),点M到点P的距离是它到点Q的距离的
,求点M的轨迹方程.
| 1 |
| 2 |
考点:轨迹方程
专题:计算题,直线与圆
分析:利用P(2,0),Q(8,0),点M到点P的距离是它到点Q的距离的
,建立方程,即可求点M的轨迹方程,
| 1 |
| 2 |
解答:
解:设M(x,y),则依条件得
=
…8
两边平方,整理得x2+y2=16,这就是所求的轨迹方程….12
| ||
|
| 1 |
| 2 |
两边平方,整理得x2+y2=16,这就是所求的轨迹方程….12
点评:本题考查圆的方程,考查两点间距离公式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
一个等比数列的前三项的积为3,最后三项的积为9,且所有项的积为729,则该数列的项数是( )
| A、13 | B、12 | C、11 | D、10 |
已知圆O:x2+y2=5和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积为( )
| A、5 | ||
| B、10 | ||
C、
| ||
D、
|
若点(1,2)到直线x-y+a=0的距离为
,则a的值为( )
| ||
| 2 |
| A、-2或2 | ||||
B、
| ||||
| C、2或0 | ||||
| D、-2或0 |
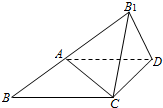 已知四边形ABCD是矩形,BC=
已知四边形ABCD是矩形,BC=