题目内容
17.四边形ABCD中,∠BAC=90°,BD+CD=2,则它的面积最大值等于$\frac{1+\sqrt{2}}{2}$.分析 由题意,当D在BC的正上方时S△DBC面积最大,A为BC的正下方时S△ABC面积最大,设BC为2x,可求DH=$\sqrt{1-{x}^{2}}$,S四边形ABCD=x2+x$\sqrt{1-{x}^{2}}$,设x=sinθ,则利用三角函数恒等变换的应用化简可得S四边形=$\frac{1}{2}$[1+$\sqrt{2}$sin(2θ-$\frac{π}{4}$)],利用正弦函数的性质即可求得S四边形的最大值.
解答 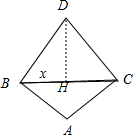 解:∵∠BAC=90°,BD+CD=2,
解:∵∠BAC=90°,BD+CD=2,
∴D在以BC为焦点的椭圆上运动,A在以BC为直径的圆上运动,
∴当D在BC的正上方时S△DBC面积最大,A为BC的正下方时S△ABC面积最大,此时,设BC为2x,则DH=$\sqrt{1-{x}^{2}}$,
∴S四边形ABCD=S△BCD+SABC=x$•\sqrt{1-{x}^{2}}$+$\frac{1}{2}•2x•x$=x2+x$\sqrt{1-{x}^{2}}$,
设x=sinθ,则$\sqrt{1-{x}^{2}}$=cosθ,
∴S四边形=sin2θ+sinθcosθ=$\frac{1}{2}$(2sin2θ+2sinθcosθ)=$\frac{1}{2}$(1-cos2θ+sin2θ)=$\frac{1}{2}$[1+$\sqrt{2}$sin(2θ-$\frac{π}{4}$)],
∴当sin(2θ-$\frac{π}{4}$)=1时,即θ=$\frac{3π}{8}$时,S四边形取得最大值,最大值为:$\frac{1+\sqrt{2}}{2}$.
故答案为:$\frac{1+\sqrt{2}}{2}$.
点评 本题主要考查了圆和椭圆的性质,考查了三角函数恒等变换的应用以及正弦函数的性质的综合应用,考查了运动思想,转化思想和数形结合思想,属于中档题.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | 异面 | B. | 平行 | C. | 相交 | D. | 相交或异面 |
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
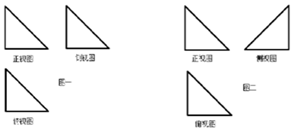 小明在解决三视图还原问题时,错把图一的三视图看成图二的三视图,假设图一所对应几何体中最大的面积为S1,图二所对应几何体中最大面的面积为S2,三视图中所有三角形均为全等的等腰直角三角形,则$\frac{{S}_{1}}{{S}_{2}}$=( )
小明在解决三视图还原问题时,错把图一的三视图看成图二的三视图,假设图一所对应几何体中最大的面积为S1,图二所对应几何体中最大面的面积为S2,三视图中所有三角形均为全等的等腰直角三角形,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | 1 | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |