题目内容
 如图5所示,在三棱锥
如图5所示,在三棱锥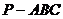 中,
中,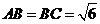 ,平面
,平面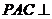 平面
平面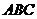 ,
,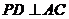 于点
于点 ,
,
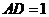 ,
,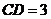 ,
,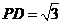 .
.
(1)证明△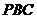 为直角三角形;
为直角三角形;
(2)求直线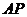 与平面
与平面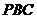 所成角的正弦值.
所成角的正弦值.
(本小题主要考查空间线面关系、直线与平面所成角、空间向量及坐标运算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)
(1)证明1:因为平面 平面
平面 ,平面
,平面 平面
平面 ,
,
 平面
平面 ,
, ,
,
所以 平面
平面 .…………………………………………………………………………………1分
.…………………………………………………………………………………1分
记 边上的中点为
边上的中点为 ,在△
,在△ 中,
中, ,所以
,所以 .
.
因为 ,
, ,所以
,所以 .………………3分
.………………3分
 因为
因为
 ,所以△
,所以△ 为直角三角形.
为直角三角形.
因为 ,
, ,
,
所以 .………4分
.………4分
连接 ,在
,在 △
△ 中,因为
中,因为 ,
, ,
,
所以 .…………5分
.…………5分
因为 平面
平面 ,
, 平面
平面 ,所以
,所以
 .
.
在 △
△ 中,因为
中,因为 ,
, ,
,
所以 .………………………………6分
.………………………………6分
在 中,因为
中,因为 ,
, ,
, ,
,
所以 .
.
所以 为直角三角形.……………………………………………………7分
为直角三角形.……………………………………………………7分
证明2:因为平面 平面
平面 ,平面
,平面 平面
平面 ,
,
 平面
平面 ,
, ,
,
所以 平面
平面 .……………………………………………………1分
.……………………………………………………1分
记 边上的中点为
边上的中点为 ,在△
,在△ 中,因为
中,因为 ,所以
,所以 .
.
因为 ,
, ,所以
,所以 .………………3分
.………………3分
连接 ,在
,在 △
△ 中,因为
中,因为 ,
, ,
, ,
,
所以 .………………………………4分
.………………………………4分
在△ 中,因为
中,因为 ,
, ,
, ,
,
所以 ,所以
,所以 .………………………………………5分
.………………………………………5分
因为 平面
平面 ,
, 平面
平面 ,
,
所以 .…………………………………………………………6分
.…………………………………………………………6分
因为 ,所以
,所以 平面
平面 .
.
因为 平面
平面 ,所以
,所以 .
.
所以 为直角三角形.……………………………………………………7分
为直角三角形.……………………………………………………7分
(2)解法1:过点 作平面
作平面 的垂线,垂足为
的垂线,垂足为 ,连
,连 ,
,
则 为直线
为直线 与平面
与平面 所成的角.…………………………………8分
所成的角.…………………………………8分
由(1)知,△ 的面积
的面积 .…………………9分
.…………………9分
因为 ,所以
,所以
 .…………………………10分
.…………………………10分
由(1)知 为直角三角形,
为直角三角形, ,
, ,
,
所以△ 的面积
的面积 .…………………11分
.…………………11分
因为三棱锥 与三棱锥
与三棱锥 的体积相等,即
的体积相等,即 ,
,
即 ,所以
,所以 .……………………………………12分
.……………………………………12分
在 △
△ 中,因为
中,因为 ,
, ,
,
所以 .………………………………13分
.………………………………13分
因为 .
.
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .…………………………………………………14分
.…………………………………………………14分
解法2:过点 作
作 ,设
,设 ,
,
 则
则 与平面
与平面 所成的角等于
所成的角等于 与平面
与平面 所成的角.……………………………………8分
所成的角.……………………………………8分
由(1)知 ,
, ,且
,且 ,
,
所以 平面
平面 .
.
因为 平面
平面 ,
,
所以平面 平面
平面 .
.
过点 作
作 于点
于点 ,连接
,连接 ,
,
则 平面
平面 .
.
所以 为直线
为直线 与平面
与平面 所成的角.……10分
所成的角.……10分
在 △
△ 中,因为
中,因为 ,
, ,
,
所以 .……………………………………11分因为
.……………………………………11分因为 ,所以
,所以 ,即
,即 ,所以
,所以 .………………………………12分
.………………………………12分
由(1)知 ,
, ,且
,且 ,
,
所以 .……………………………………13分
.……………………………………13分
因为 ,
,
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .…………………………………………………14分
.…………………………………………………14分
 解法3:延长
解法3:延长 至点
至点 ,使得
,使得 ,连接
,连接 、
、 ,……………………………………8分
,……………………………………8分
在△ 中,
中, ,
,
所以 ,即
,即 .
.
在△ 中,因为
中,因为 ,
, ,
, ,
,
所以 ,
,
所以 .
.
因为 ,
,
所以 平面
平面 .…………………………………………………………………………………9分
.…………………………………………………………………………………9分
过点 作
作 于点
于点 ,
,
因为 平面
平面 ,
,
所以 .
.
因为 ,
,
所以 平面
平面 .
.
所以 为直线
为直线 与平面
与平面 所成的角.……………………………………………………11分
所成的角.……………………………………………………11分
由(1)知, ,
,
所以 .
.
在△ 中,点
中,点 、
、 分别为边
分别为边 、
、 的中点,
的中点,
所以 .………………………………………………………12分
.………………………………………………………12分
在△ 中,
中, ,
, ,
, ,
,
所以 ,即
,即 .……………………………………………………………13分
.……………………………………………………………13分
因为 .
.
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .…………………………………………………14分
.…………………………………………………14分
解法4:以点 为坐标原点,以
为坐标原点,以 ,
, 所在的直线分别为
所在的直线分别为 轴,
轴, 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系 ,……………………………………………………………………8分
,……………………………………………………………………8分
 则
则 ,
, ,
, ,
, .
.
于是 ,
, ,
, .
.
设平面 的法向量为
的法向量为 ,
,
则
即
取 ,则
,则 ,
, .
.
所以平面 的一个法向量为
的一个法向量为 .………………………………12分
.………………………………12分
设直线 与平面
与平面 所成的角为
所成的角为 ,
,
则 .
.
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .………………………………14分
.………………………………14分
若第(1)、(2)问都用向量法求解,给分如下:
 (1)以点
(1)以点 为坐标原点,以
为坐标原点,以 ,
, 所在的直线分别为
所在的直线分别为 轴,
轴, 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系 ,……………………………………………………………………………1分
,……………………………………………………………………………1分
则 ,
, ,
, .
.
于是 ,
, .
.
因为 ,
,
所以 .
.
所以 .
.
所以 为直角三角形.…………………………………………………………7分
为直角三角形.…………………………………………………………7分
(2)由(1)可得, .
.
于是 ,
, ,
, .
.
设平面 的法向量为
的法向量为 ,
,
则 即
即
取 ,则
,则 ,
, .
.
所以平面 的一个法向量为
的一个法向量为 .…………………………………12分
.…………………………………12分
设直线 与平面
与平面 所成的角为
所成的角为 ,
,
则 .
.
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .……………………………14分
.……………………………14分

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 (1) 证明:
(1) 证明:
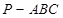 中,
中,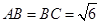 ,平面
,平面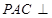 平面
平面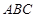 ,
,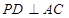 于点
于点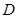 ,
,
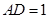 ,
,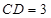 ,
,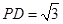 .
.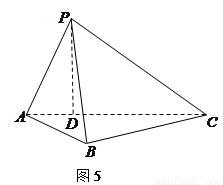
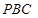 为直角三角形;
为直角三角形;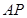 与平面
与平面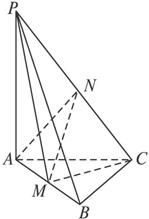
 如图5所示,在三棱锥
如图5所示,在三棱锥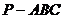 中,
中,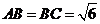 ,平面
,平面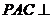 平面
平面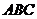 ,
,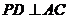 于点
于点 ,
,
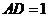 ,
,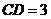 ,
,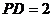 .
. 为直角三角形.
为直角三角形.