题目内容
 如图5所示,在三棱锥
如图5所示,在三棱锥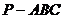 中,
中,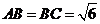 ,平面
,平面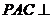 平面
平面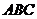 ,
,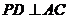 于点
于点 ,
,
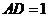 ,
,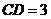 ,
,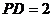 .
.
(1)求三棱锥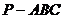 的体积;
的体积;
(2)证明△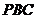 为直角三角形.
为直角三角形.
【答案】
(本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)
(1)证明:因为平面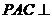 平面
平面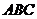 ,平面
,平面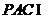 平面
平面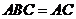 ,
,  平面
平面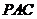 ,
, ,
,
所以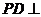 平面
平面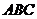 .…………………………………………………………………………………2分
.…………………………………………………………………………………2分
记 边上的中点为
边上的中点为 ,在△
,在△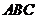 中,因为
中,因为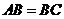 ,
,
所以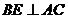 .
.
因为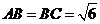 ,
,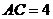 ,
,
所以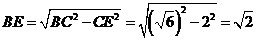 .………………………………………………………4分
.………………………………………………………4分
所以△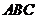 的面积
的面积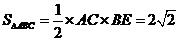 .……………………………………………………5分
.……………………………………………………5分
因为 ,
,
所以三棱锥 的体积
的体积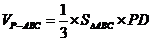
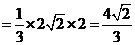 .……………………7分
.……………………7分
(2)证法1:因为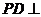
 ,所以△
,所以△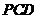 为直角三角形.
为直角三角形.
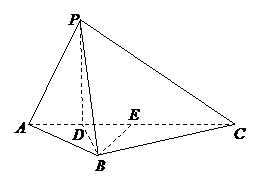 因为
因为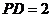 ,
,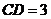 ,
,
所以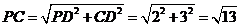 .………………9分
.………………9分
连接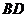 ,在
,在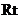 △
△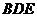 中,
中,
因为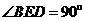 ,
,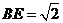 ,
,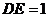 ,
,
所以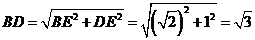 .…………10分
.…………10分
由(1)知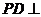 平面
平面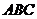 ,又
,又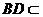 平面
平面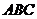 ,
,
所以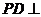
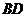 .
.
在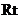 △
△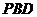 中,因为
中,因为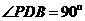 ,
,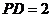 ,
,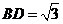 ,
,
所以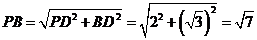 .……………………………………………………12分
.……………………………………………………12分
在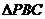 中,因为
中,因为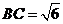 ,
,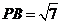 ,
,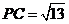 ,
,
所以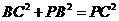 .………………………………………………………………………………13分
.………………………………………………………………………………13分
所以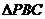 为直角三角形.……………………………………………………………………………14分
为直角三角形.……………………………………………………………………………14分
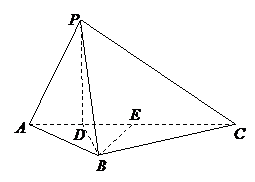 证法2:连接
证法2:连接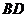 ,在
,在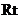 △
△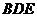 中,因为
中,因为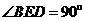 ,
,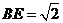 ,
,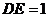 ,
,
所以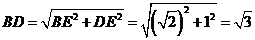 .…………8分
.…………8分
在△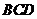 中,
中,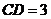 ,
,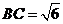 ,
,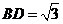 ,
,
所以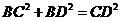 ,所以
,所以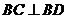 .………………10分
.………………10分
由(1)知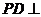 平面
平面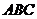 ,
,
因为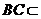 平面
平面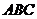 ,
,
所以 .
.
因为 ,
,
所以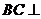 平面
平面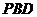 .…………………………………………………………………………………12分
.…………………………………………………………………………………12分
因为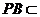 平面
平面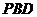 ,所以
,所以 .
.
所以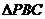 为直角三角形.……………………………………………………………………………14分
为直角三角形.……………………………………………………………………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1) 证明:
(1) 证明:
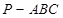 中,
中,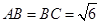 ,平面
,平面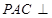 平面
平面 ,
,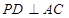 于点
于点 ,
,
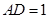 ,
,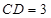 ,
,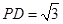 .
.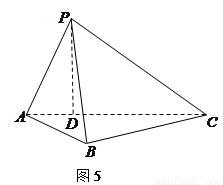
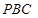 为直角三角形;
为直角三角形;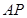 与平面
与平面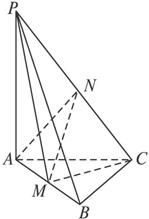
 如图5所示,在三棱锥
如图5所示,在三棱锥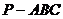 中,
中,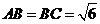 ,平面
,平面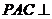 平面
平面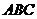 ,
,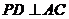 于点
于点 ,
,
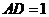 ,
,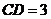 ,
,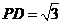 .
.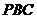 为直角三角形;
为直角三角形;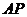 与平面
与平面