题目内容
如图5所示,在三棱锥P—ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.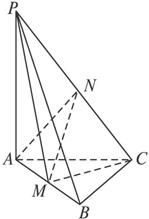
图5
(1)证明平面PAB⊥平面PCM;
(2)证明线段PC的中点为球O的球心;
(3)若球O的表面积为25π,求三棱锥P—ABC的体积.
(1)证明:∵AC=BC,M为AB的中点,
∴CM⊥AB.∵PA⊥平面ABC,CM![]() 平面ABC,∴PA⊥CM.
平面ABC,∴PA⊥CM.
∵AB∩PA=A,AB![]() 平面PAB,PA
平面PAB,PA![]() 平面PAB,∴CM⊥平面PAB.
平面PAB,∴CM⊥平面PAB.
∵CM![]() 平面PCM,∴平面PAB⊥平面PCM.
平面PCM,∴平面PAB⊥平面PCM.
(2)证明:由(1)知CM⊥平面PAB.

∵PM![]() 平面PAB,∴CM⊥PM.
平面PAB,∴CM⊥PM.
∵PA⊥平面ABC,AC![]() 平面ABC,∴PA⊥AC.
平面ABC,∴PA⊥AC.
取PC的中点N,连接MN、AN.
在Rt△PAC中,点N为斜边PC的中点,∴AN=PN=NC.
在Rt△PCM中,点N为斜边PC的中点.∴MN=PN=NC.
∴PN=NC=AN=MN.∴点N是球O的球心,即线段PC的中点为球O的球心.
(注:本题答案中符号“![]() ”等价于“
”等价于“![]() ”)
”)
(3)解:依题意得4π·NC2=25π,解得NC=![]() .
.
∴PC=5,PA=![]() =
=![]() =4.
=4.
∵AB=AC=BC=3,∴△ABC的面积S△ABC=![]() ×32=
×32=![]() .
.
∴三棱锥P—ABC的体积为V=![]() ×S△ABC×PA=
×S△ABC×PA=![]() ×
×![]() ×4=3
×4=3![]() .
.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 (1) 证明:
(1) 证明:
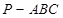 中,
中,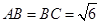 ,平面
,平面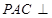 平面
平面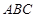 ,
,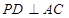 于点
于点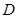 ,
,
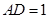 ,
,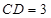 ,
,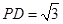 .
.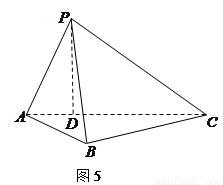
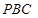 为直角三角形;
为直角三角形;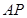 与平面
与平面 如图5所示,在三棱锥
如图5所示,在三棱锥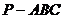 中,
中,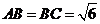 ,平面
,平面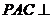 平面
平面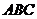 ,
,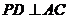 于点
于点 ,
,
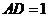 ,
,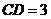 ,
,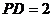 .
.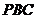 为直角三角形.
为直角三角形. 如图5所示,在三棱锥
如图5所示,在三棱锥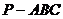 中,
中,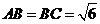 ,平面
,平面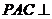 平面
平面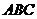 ,
,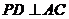 于点
于点 ,
,
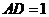 ,
,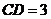 ,
,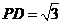 .
.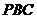 为直角三角形;
为直角三角形;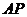 与平面
与平面