题目内容
(本小题满分14分)
如图5所示,在三棱锥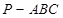 中,
中,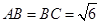 ,平面
,平面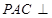 平面
平面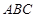 ,
,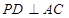 于点
于点 ,
,
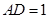 ,
,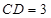 ,
,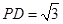 .
.
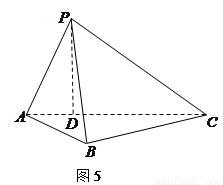
(1)证明△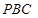 为直角三角形;
为直角三角形;
(2)求直线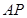 与平面
与平面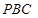 所成角的正弦值
所成角的正弦值
(1)证明1:因为平面 平面
平面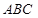 ,平面
,平面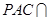 平面
平面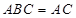 ,
,
 平面
平面 ,
,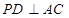 ,
,
所以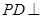 平面
平面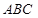 .
.
记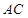 边上的中点为
边上的中点为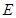 ,在△
,在△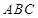 中,
中, ,所以
,所以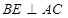 .
.
因为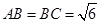 ,
,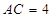 ,所以
,所以 .
.
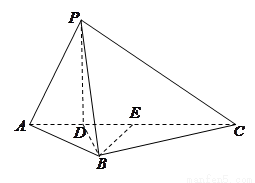
因为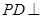
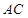 ,所以△
,所以△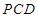 为直角三角形.
为直角三角形.
因为 ,
,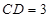 ,[来源:ZXXK]
,[来源:ZXXK]
所以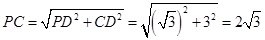 .
.
连接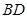 ,在
,在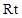 △
△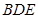 中,因为
中,因为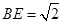 ,
,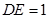 ,
,
所以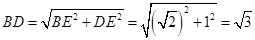 .
.
因为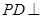 平面
平面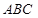 ,
,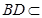 平面
平面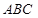 ,所以
,所以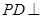
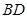 .
.
在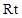 △
△ 中,因为
中,因为 ,
,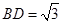 ,
,
所以 .
.
在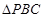 中,因为
中,因为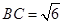 ,
,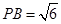 ,
, ,
,
所以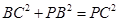 .
.
所以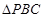 为直角三角形.
为直角三角形.
证明2:因为平面 平面
平面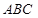 ,平面
,平面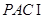 平面
平面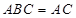 ,
,
 平面
平面 ,
,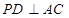 ,
,
所以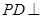 平面
平面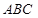 .
.
记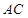 边上的中点为
边上的中点为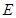 ,在△
,在△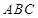 中,因为
中,因为 ,所以
,所以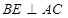 .
.
因为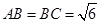 ,
,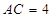 ,所以
,所以 .
.
连接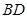 ,在
,在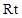 △
△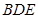 中,因为
中,因为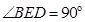 ,
,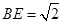 ,
,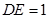 ,
,
所以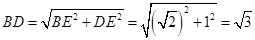 .
.
在△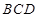 中,因为
中,因为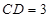 ,
,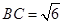 ,
,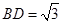 ,
,
所以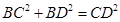 ,所以
,所以 .
.
因为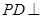 平面
平面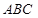 ,
,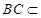 平面
平面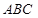 ,
,
所以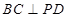 .
.
因为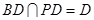 ,所以
,所以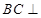 平面
平面 .
.
因为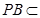 平面
平面 ,所以
,所以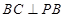 .
.
所以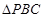 为直角三角形.
为直角三角形.
(2)解法1:过点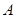 作平面
作平面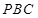 的垂线,垂足为
的垂线,垂足为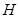 ,连
,连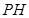 ,
,
则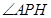 为直线
为直线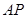 与平面
与平面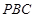 所成的角.
所成的角.
由(1)知,△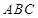 的面积
的面积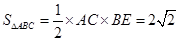 .
.
因为 ,所以
,所以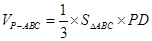
 .
.
由(1)知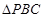 为直角三角形,
为直角三角形,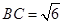 ,
,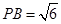 ,
,
所以△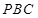 的面积
的面积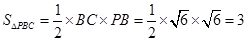 .
.
因为三棱锥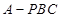 与三棱锥
与三棱锥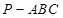 的体积相等,即
的体积相等,即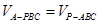 ,
,
即 ,所以
,所以 .
.
在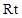 △
△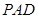 中,因为
中,因为 ,
, ,
,
所以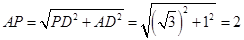 .
.
因为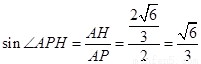 .
.
所以直线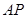 与平面
与平面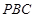 所成角的正弦值为
所成角的正弦值为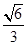 .
.
解法2:过点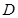 作
作 ,设
,设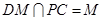 ,
,

则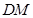 与平面
与平面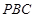 所成的角等于
所成的角等于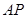 与平面
与平面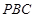 所成的角.
所成的角.
由(1)知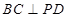 ,
,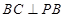 ,且
,且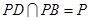 ,
,
所以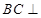 平面
平面 .
.
因为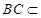 平面
平面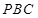 ,
,
所以平面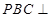 平面
平面 .
.
过点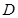 作
作 于点
于点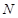 ,连接
,连接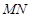 ,
,
则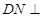 平面
平面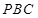 .
.
所以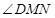 为直线
为直线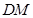 与平面
与平面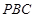 所成的角.
所成的角.
在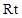 △
△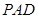 中,因为
中,因为 ,
, ,
,
所以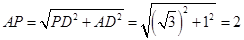 .
.
因为 ,所以
,所以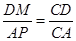 ,即
,即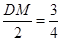 ,所以
,所以 .
.
由(1)知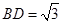 ,
,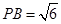 ,且
,且 ,
,
所以 .
.
因为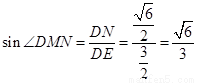 ,
,
所以直线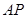 与平面
与平面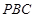 所成角的正弦值为
所成角的正弦值为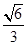 .
.
解法3:延长 至点
至点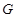 ,使得
,使得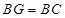 ,连接
,连接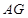 、
、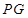 ,
,
在△ 中,
中, ,
,

所以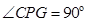 ,即
,即 .
.
在△ 中,因为
中,因为 ,
, ,
,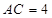 ,
,
所以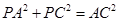 ,
,
所以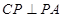 .
.
因为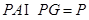 ,
,
所以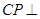 平面
平面 .
.
过点 作
作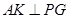 于点
于点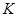 ,
,
因为 平面
平面 ,
,
所以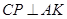 .
.
因为 ,
,
所以 平面
平面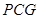 .
.
所以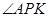 为直线
为直线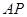 与平面
与平面 所成的角.
所成的角.
由(1)知,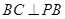 ,
,
所以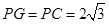 .
.
在△ 中,点
中,点 、
、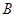 分别为边
分别为边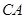 、
、 的中点,
的中点,
所以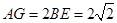 .
.
在△ 中,
中,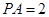 ,
,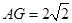 ,
, ,
,
所以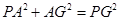 ,即
,即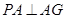 .
.
因为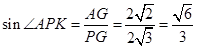 .
.
所以直线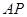 与平面
与平面 所成角的正弦值为
所成角的正弦值为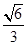 .
.
解法4:以点 为坐标原点,以
为坐标原点,以 ,
,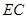 所在的直线分别为
所在的直线分别为 轴,
轴,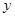 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系 ,
,

则 ,
, ,
,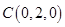 ,
, .
.
于是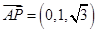 ,
, ,
,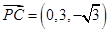 .
.
设平面 的法向量为
的法向量为 ,
,
则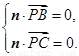
即
取 ,则
,则 ,
,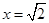 .
.
所以平面 的一个法向量为
的一个法向量为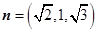 .
.
设直线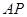 与平面
与平面 所成的角为
所成的角为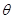 ,
,
则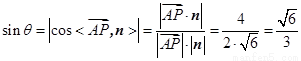 .
.
所以直线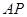 与平面
与平面 所成角的正弦值为
所成角的正弦值为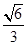 .
.
若第(1)、(2)问都用向量法求解,给分如下:

(1)以点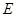 为坐标原点,以
为坐标原点,以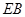 ,
,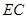 所在的直线分别为
所在的直线分别为 轴,
轴,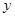 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系 ,
,
则 ,
,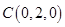 ,
, .
.
于是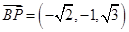 ,
,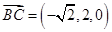 .
.
因为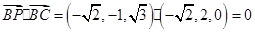 ,
,
所以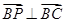 .
.
所以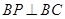 .
.
所以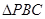 为直角三角形.
为直角三角形.
(2)由(1)可得, .
.
于是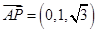 ,
, ,
,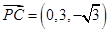 .
.
设平面 的法向量为
的法向量为 ,
,
则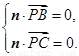 即
即
取 ,则
,则 ,
,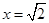 .
.
所以平面 的一个法向量为
的一个法向量为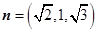 .
.
设直线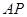 与平面
与平面 所成的角为
所成的角为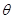 ,
,
则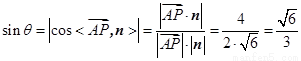 .
.
所以直线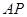 与平面
与平面 所成角的正弦值为
所成角的正弦值为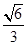 .
.
【解析】略

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)