题目内容
 某几何体的三视图如图,则该几何体的表面积等于
某几何体的三视图如图,则该几何体的表面积等于考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:几何体是一个四棱锥,四棱锥的底面是一个长为6,宽为2的矩形,顶点底面的面积,四棱锥的一个侧面与底面垂直,四棱锥的高是4,根据勾股定理做出三角形的高,做出4个三角形的面积,求和得到结果.
解答:
解:由三视图知,几何体是一个四棱锥,
∵四棱锥的底面是一个长为6,宽为2的矩形,
∴面积是6×2=12,
∵四棱锥的后侧面与底面垂直,
顶点在底面上的射影是垂直于底面的这条棱与底面的交线的中点,
四棱锥的高是4,
前侧面的高是
=2
,
左右两个侧面的高为
=5,
∴四个侧面的面积是
×6×2
+
×6×4+2×
×2×5=34+6
,
故答案为:34+6
∵四棱锥的底面是一个长为6,宽为2的矩形,
∴面积是6×2=12,
∵四棱锥的后侧面与底面垂直,
顶点在底面上的射影是垂直于底面的这条棱与底面的交线的中点,
四棱锥的高是4,
前侧面的高是
| 22+42 |
| 5 |
左右两个侧面的高为
| 32+42 |
∴四个侧面的面积是
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
故答案为:34+6
| 5 |
点评:本题考查了由三视图求几何体的表面积,根据三视图判断几何体的结构特征及求相关几何量的数据是解答本题的关键.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则这个几何体的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式
<0的解集为( )
| 7x2-6x-1 |
| x2-x+1 |
| A、空集 | ||
B、{x|-
| ||
C、{x|-1<x<
| ||
D、{x|x<-
|
已知命题p:“?x∈[1,2],x2-a≥0”,命题q:“?x∈R,x2+2ax+2-a=0”.若命题“p且q”是真命题,则实数a的取值范围为( )
| A、-2≤a≤1 |
| B、a≤-2或1≤a≤2 |
| C、a≥1 |
| D、a≤-2或 a=1 |
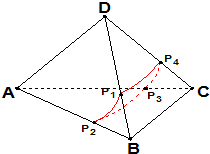 如图,四面体ABCD中,DA=DB=DC=1,且DA、DB、DC两两互相垂直,在该四面体表面上与点A距离是
如图,四面体ABCD中,DA=DB=DC=1,且DA、DB、DC两两互相垂直,在该四面体表面上与点A距离是