题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{2x-1(x>-1)}\\{{e}^{x}(x≤-1)}\end{array}\right.$,若a<b,f(a)=f(b),则实数a-2b的取值范围为( )| A. | $({-∞,\frac{1}{e}-1})$ | B. | $({-∞,-\frac{1}{e}})$ | C. | $({-∞,-\frac{1}{e}-2})$ | D. | $({-∞,-\frac{1}{e}-2}]$ |
分析 画出函数f(x)=$\left\{\begin{array}{l}{2x-1(x>-1)}\\{{e}^{x}(x≤-1)}\end{array}\right.$的图象,结合a<b,且f(a)=f(b),表示出a-2b,利用导数法求出其上确界,可得答案.
解答 解:函数f(x)=$\left\{\begin{array}{l}{2x-1(x>-1)}\\{{e}^{x}(x≤-1)}\end{array}\right.$的图象如下图所示: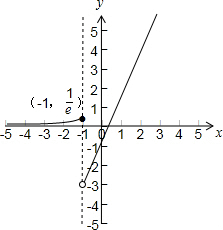
若a<b,f(a)=f(b),
则2b-1=ea,则a-2b=a-ea-1,a≤-1,
令y=a-ea-1,a≤-1,
则y′=1-ea,a≤-1,
此时ea≤
| 1 |
| e |
故y=a-ea-1<y|a=-1=-
| 1 |
| e |
即实数a-2b的取值范围为(-∞,-
| 1 |
| e |
故选:D.
点评 本题考查的知识点是分段函数的应用,根据已知画出函数f(x)的图象,是解答的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
7.下列各函数在其定义域中,既是奇函数,又是增函数的是( )
| A. | y=x+1 | B. | y=-x3 | C. | y=-$\frac{1}{x}$ | D. | y=x|x| |
5.若集合A={x|x2-6x+8<0},集合B={x∈N|y=$\sqrt{3-x}$},则A∩B=( )
| A. | {3} | B. | {1,3} | C. | {1,2} | D. | {1,2,3} |
12.若sinθ=$\frac{k+1}{k-3}$,cosθ=$\frac{k-1}{k-3}$,且θ的终边不落在坐标轴上,则tanθ的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{4}$或0 | C. | 0 | D. | 以上答案都不对 |
2.命题:“对任意的x∈R,x2+x+1>0”的否定是( )
| A. | 不存在x∈R,x2+x+1>0 | B. | 存在x0∈R,x02+x0+1>0 | ||
| C. | 存在x0∈R,x02+x0+1≤0 | D. | 对任意的x∈R,x2+x+1≤0 |
9.位于平面直角坐标系原点的一个质点P按下列规则移动:质点每次移动一个单位,移动的方向是向上或向下,并且向上移动的概率为$\frac{1}{4}$,则质点P移动4次后位于点(0,2)的概率是( )
| A. | $\frac{1}{256}$ | B. | $\frac{3}{256}$ | C. | $\frac{9}{256}$ | D. | $\frac{3}{64}$ |