题目内容
8.2012年全国中学生机器人大赛选选拔赛中,机器人刚开始在原点位置,为了让机器人完成某项任务,学生给机器人设置了以下指令:先逆时针旋转α角,然后向前进1米,将该指令进行一次称为一次操作,试用向量解决以下问题.(1)当α=$\frac{π}{3}$时,经过几次操作才能回到原点?
(2)是否存在α,使机器人经过10次操作,能首次回到原点?
分析 (1)如图所示,当α=$\frac{π}{3}$时,经过1次操作到A1点,经过2次操作到A2点,利用多边形外角和定理及其向量多边形法则即可得出.
(2)根据多边形外角和定理α=$\frac{2π}{10}$.
解答 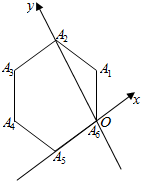 解:(1)如图所示,
解:(1)如图所示,
当α=$\frac{π}{3}$时,经过1次操作到A1点,经过2次操作到A2点,
6α=2π(多边形外角和定理).
∴$\overrightarrow{O{A}_{1}}$+$\overrightarrow{{A}_{1}{A}_{2}}$+…+$\overrightarrow{{A}_{5}{A}_{6}}$=$\overrightarrow{0}$,
因此当α=$\frac{π}{3}$时,经过6次操作才能回到原点.
(2)根据多边形外角和定理α=$\frac{2π}{10}$=$\frac{π}{5}$.
∴存在α=$\frac{π}{5}$,使机器人经过10次操作,能首次回到原点.
点评 本题考查了多边形外角和定理、向量的多边形法则,考查了数形结合方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.-456°角的终边相同的角的集合是( )
| A. | {α|α=k•360°+456°,k∈Z} | B. | {α|α=k•360°+264°,k∈Z} | ||
| C. | {α|α=k•360°+96°,k∈Z} | D. | {α|α=k•360°-264°,k∈Z} |
16.已知集合A={x|-1<x<2},集合B={x|0<x<1},则有( )
| A. | A⊆B | B. | A?B | C. | B?A | D. | A=B |
3.下列函数中,在其定义域内既是奇函数又是减函数的是( )
| A. | y=x | B. | y=$\frac{1}{x}$ | C. | y=-x3 | D. | y=($\frac{1}{2}$)x |
13.在等差数列{an}中,已知a3+a5=2,a7+a10+a13=9,则此数列的公差为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
17.已知函数f(x)=$\left\{\begin{array}{l}{2x-1(x>-1)}\\{{e}^{x}(x≤-1)}\end{array}\right.$,若a<b,f(a)=f(b),则实数a-2b的取值范围为( )
| A. | $({-∞,\frac{1}{e}-1})$ | B. | $({-∞,-\frac{1}{e}})$ | C. | $({-∞,-\frac{1}{e}-2})$ | D. | $({-∞,-\frac{1}{e}-2}]$ |
18.已知命题p:?x∈R,x2-2x+4≤0,则?p为( )
| A. | ?x∈R,x2-2x+4≥0 | B. | $?{x_0}∈R,x_0^2-2{x_0}+4>0$ | ||
| C. | ?x∉R,x2-2x+4≤0 | D. | $?{x_0}∉R,x_0^2-2{x_0}+4>0$ |