题目内容
6.若复数z满足2z-$\overline{z}$=2+3i(i为虚数单位),则|z|=( )| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{13}$ | D. | 13 |
分析 根据复数的四则运算法则先求出复数z,再计算它的模长.
解答 解:复数z=a+bi,a、b∈R;
∵2z-$\overline{z}$=2+3i,
∴2(a+bi)-(a-bi)=2+3i,
即$\left\{\begin{array}{l}{2a-a=2}\\{2b+b=3}\end{array}\right.$,
解得a=2,b=1,
∴z=2+i,
∴|z|=$\sqrt{{2}^{2}{+1}^{2}}$=$\sqrt{5}$.
故选:A.
点评 本题主要考查了复数的计算问题,要求熟练掌握复数的四则运算以及复数长度的计算公式,是基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
16.已知集合A={-1,0,1,2},B={x|x2-x-2≤0},则x∈A是x∈B的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.设a,b,l均为直线,α,β均为平面,则下列命题判断错误的是( )
| A. | 若l∥α,则α内存在无数条直线与l平行 | |
| B. | 若α⊥β,则α内存在无数条直线与β不垂直 | |
| C. | 若α∥β,则α内存在直线m,β内存在直线,使得m⊥n | |
| D. | 若a⊥l,b⊥l,则a与b不可能垂直 |
18.已知x,y满足约束条件$\left\{\begin{array}{l}2x+y-3≥0\\ x-y≤0\\ x-3≤0\end{array}\right.$,则目标函数z=2x-3y的最大值是( )
| A. | 15 | B. | 5 | C. | -1 | D. | -3 |
15.下列函数中值域为实数集的偶函数是( )
| A. | f(x)=|lnx|(x>0) | B. | f(x)=ln|x|(x≠0) | C. | f(x)=x-$\frac{1}{x}$(x≠0) | D. | f(x)=x+$\frac{1}{x}$(x≠0) |
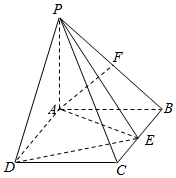 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.