题目内容
16.实数x1,x2,x3,…x1008…x2015,满足0≤x1≤x2≤x3≤…≤x1008≤…≤x2015≤13如果它们的平方组成公差$d=\frac{72}{1007}$的等差数列,当|x1-x2|+|x2-x3|+…+|x2014-x2015|取最小值时,x1008=$\sqrt{97}$.分析 由题意,|x1-x2|+|x2-x3|+…+|x2014-x2015|=x2-x1+x3-x2+…+x2015-x2014=x2015-x1,利用平方组成公差$d=\frac{72}{1007}$的等差数列,可得x20152=x12+2014×$\frac{72}{1007}$=x12+144≤169,0≤x1≤5,确定x1=5,x2015=13时,取得最小值8,即可求出x1008.
解答 解:由题意,|x1-x2|+|x2-x3|+…+|x2014-x2015|=x2-x1+x3-x2+…+x2015-x2014=x2015-x1,
∵平方组成公差$d=\frac{72}{1007}$的等差数列,
∴x20152=x12+2014×$\frac{72}{1007}$=x12+144≤169,
∴0≤x1≤5,
x2015-x1=$\sqrt{{{x}_{1}}^{2}+144}$-x1=$\frac{144}{\sqrt{{{x}_{1}}^{2}+144}+{x}_{1}}$
在x1=5,x2015=13时,取得最小值8
∴x10082=x12+1007×$\frac{72}{1007}$=97,
∴x1008=$\sqrt{97}$.
故答案为:$\sqrt{97}$.
点评 本题考查等差数列的性质,考查学生的计算能力,确定x1=5,x2015=13时,取得最小值是关键.

练习册系列答案
相关题目
5.已知cosA+cosB=0,sinA+sinB=1,则cos(A+B)的值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |
11.已知集合A={0,x},B={x2,-x2,|x|-1},若A⊆B,则实数x的值为( )
| A. | 1或-1 | B. | 1 | C. | -1 | D. | 2 |
8.若集合A={x|2x<5},集合B={-1,0,1,3},则A∩B等于( )
| A. | {0,1} | B. | {-1,0,1} | C. | {0,1,3} | D. | {-1,0,1,3} |
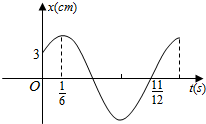 如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求:
如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求: