题目内容
1.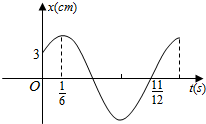 如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求:
如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求:(1)函数解析式;
(2)单摆摆动到最右边时,离开平衡位置的距离是多少?
(3)单摆来回摆动一次需要多长时间?
分析 (1)求出解析式中的参数,即可求出函数解析式;
(2)A=6,可得单摆摆动到最右边时,离开平衡位置的距离;
(3)T=1,可得单摆来回摆动一次需要的时间.
解答 解:(1)由题意,$\frac{11}{12}$-$\frac{1}{6}$=$\frac{3}{4}$T,∴T=1,
∴$\frac{2π}{ω}$=1,∴ω=2π,
∵t=$\frac{1}{6}$,s最大,
∴2π•$\frac{1}{6}$+φ=$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,
∵t=0,s=3,
∴A=6,
∴s=6sin(2πt+$\frac{π}{6}$);
(2)A=6,单摆摆动到最右边时,离开平衡位置的距离是6cm;
(3)T=1,单摆来回摆动一次需要1s.
点评 本题考查三角函数的解析式的求法与应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
10.解下列不等式:
(1)log3x>2;
(2)log${\;}_{\frac{1}{2}}$(2x-$\frac{7}{8}$)<3;
(3)2x<3;
(4)($\frac{1}{3}$)x-1<2.
(1)log3x>2;
(2)log${\;}_{\frac{1}{2}}$(2x-$\frac{7}{8}$)<3;
(3)2x<3;
(4)($\frac{1}{3}$)x-1<2.
9.下表是高三某位文科生连续5次月考的历史、政治的成绩,结果统计如下:
(1)求该生5次月考历史成绩的平均分和政治成绩的方差
(2)一般来说,学生的历史成绩与政治成绩有较强的线性相关,根据上表提供的数据,求两个变量x、y的线性回归方程$\overline{y}$=$\overline{b}$x+$\overline{a}$
(附:$\overline{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-x)({y}_{i}-y)}{\sum_{i=1}^{n}({x}_{i}-x)^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-nxy}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$,$\overline{a}$=y-$\overline{b}$x)
| 月份 | 9 | 10 | 11 | 12 | 1 |
| 历史(x分) | 79 | 81 | 83 | 85 | 87 |
| 政治(y分) | 77 | 79 | 79 | 82 | 83 |
(2)一般来说,学生的历史成绩与政治成绩有较强的线性相关,根据上表提供的数据,求两个变量x、y的线性回归方程$\overline{y}$=$\overline{b}$x+$\overline{a}$
(附:$\overline{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-x)({y}_{i}-y)}{\sum_{i=1}^{n}({x}_{i}-x)^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-nxy}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$,$\overline{a}$=y-$\overline{b}$x)
13.已知定义在R上的偶函数f(x)在[0,+∞)上递减,若不等式f(x3-x2+a)+f(-x3+x2-a)≥2f(1)对x∈[0,1]恒成立,则实数a的取值范围为( )
| A. | [$\frac{23}{27}$,1] | B. | [-$\frac{23}{27}$,1] | C. | [1,3] | D. | (-∞1] |
10.不等式${2^{{x^2}+2x-4}}≤\frac{1}{2}$的解集为( )
| A. | [-1,3] | B. | [-3,-1] | C. | [-3,1] | D. | [1,3] |