题目内容
16.已知函数f(x)=lnx+a($\frac{1}{x}$-1),其中a为大于零的常数.(1)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围;
(2)求证:对于任意的n∈N*,且n>1时,都有lnn>$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$恒成立.
分析 (1)求导,由题意可知:f′(x)≥0在[1,+∞)上恒成立,则a≤1;
(2)由a=1,则f(x)=lnx+$\frac{1}{x}$-1在[1,+∞),则f($\frac{n}{n-1}$)>f(1),则lnn-ln(n-1)>$\frac{1}{n}$,对任意n∈N*,且n>1恒成立,根据对数的运算性质,则lnn>$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$恒成立.
解答 解:(1)f(x)=lnx+a($\frac{1}{x}$-1),求导f′(x)=$\frac{x-a}{{x}^{2}}$,
由已知,f′(x)≥0在[1,+∞)上恒成立,
则a≤x在[1,+∞)上恒成立,
∴a≤1,
实数a的取值范围(0,1];
(2)证明:由(1)可知:a=1,则f(x)=lnx+$\frac{1}{x}$-1在[1,+∞)递增,
当n>1时,由$\frac{n}{n-1}$>1,则f($\frac{n}{n-1}$)>f(1),
即lnn-ln(n-1)>$\frac{1}{n}$,对任意n∈N*,且n>1恒成立,
lnn=[lnn-ln(n-1)]+[ln(n-1)-ln(n-2)]+…+[ln3-ln2]+[ln2-ln1>$\frac{1}{n}$+$\frac{1}{n-1}$+…+$\frac{1}{3}$+$\frac{1}{2}$,
∴对于任意的n∈N*,且n>1时,都有lnn>$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$恒成立.
点评 本题考查导数的综合应用,考查不等式恒成立,对数的运算性质,考查计算能力,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
11.为了得到函数$y={log_2}\frac{x+1}{4}$的图象,只需把函数y=log2x的图象上所有的点( )
| A. | 向左平移1个单位长度,再向上平移2个单位长度 | |
| B. | 向右平移1个单位长度,再向上平移2个单位长度 | |
| C. | 向左平移1个单位长度,再向下平移2个单位长度 | |
| D. | 向右平移1个单位长度,再向下平移2个单位长度 |
1.已知函数y=Asin(ωx+ϕ)+m的最大值为4,最小值为0,最小正周期为π,直线$x=\frac{π}{6}$是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
| A. | $y=4sin(2x+\frac{π}{6})$ | B. | $y=-2sin(2x+\frac{π}{6})+2$ | C. | $y=-2sin(x+\frac{π}{3})+2$ | D. | $y=2sin(2x+\frac{π}{3})+2$ |
6.若输入n=4,执行如图所示的程序框图,输出的s=( )
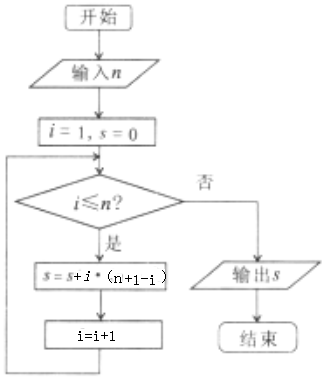

| A. | 10 | B. | 16 | C. | 20 | D. | 35 |