题目内容
19.已知函数f1(x)=x2-2|x|,f2(x)=x+2,设g(x)=$\frac{{f}_{1}(x)+{f}_{2}(x)}{2}$-$\frac{|{f}_{1}(x)-{f}_{2}(x)|}{2}$,若 a,b∈[-2,4],且当x1,x2∈[a,b](x1≠x2)时,$\frac{g({x}_{1})-g({x}_{2})}{{x}_{1}-{x}_{2}}$>0恒成立,则b-a的最大值为( )| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
分析 讨论x的范围去绝对值号,得出g(x)的解析式,利用g(x)的单调性得出区间[a,b]的范围即可得出答案.
解答 解:f1(x)=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥0}\\{{x}^{2}+2x,x<0}\end{array}\right.$,
∴f1(x)+f2(x)=$\left\{\begin{array}{l}{{x}^{2}-x+2,x≥0}\\{{x}^{2}+3x+2,x<0}\end{array}\right.$
f1(x)-f2(x)=$\left\{\begin{array}{l}{{x}^{2}-3x-2,x≥0}\\{{x}^{2}+x-2,x<0}\end{array}\right.$.
∴|f1(x)-f2(x)|=$\left\{\begin{array}{l}{-{x}^{2}+3x+2,0≤x<\frac{3+\sqrt{17}}{2}}\\{{x}^{2}-3x-2,x>\frac{3+\sqrt{17}}{2}}\\{-{x}^{2}-x+2,-2≤x<0}\\{{x}^{2}+x-2,x≤-2}\end{array}\right.$,
∴g(x)=$\left\{\begin{array}{l}{{x}^{2}-2x,0≤x≤\frac{3+\sqrt{17}}{2}}\\{x+2,x>\frac{3+\sqrt{17}}{2}或x<-2}\\{{x}^{2}+2x,-2≤x<0}\\{\;}\end{array}\right.$,
做出g(x)的函数图象如图所示: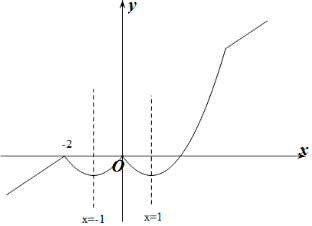
∴g(x)在(-2,-1)上是减函数,在(-1,0)上是增函数,在(-1,0)上是减函数,在(1,4)上是增函数,
∵当x1,x2∈[a,b](x1≠x2)时,$\frac{g({x}_{1})-g({x}_{2})}{{x}_{1}-{x}_{2}}$>0恒成立,
∴g(x)在[a,b]上是增函数,又 a,b∈[-2,4],
∴[a,b]⊆[-1,0]或[a,b]⊆[1,4].
∴b-a的最大值为4-1=3.
故选C.
点评 本题考查了含绝对值函数的解析式化简,函数单调性的判断,属于中档题.

| A. | 向左平移1个单位长度,再向上平移2个单位长度 | |
| B. | 向右平移1个单位长度,再向上平移2个单位长度 | |
| C. | 向左平移1个单位长度,再向下平移2个单位长度 | |
| D. | 向右平移1个单位长度,再向下平移2个单位长度 |
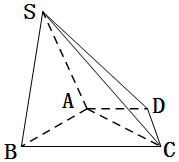 如图,如图,在四棱锥S-ABCD中,底面梯形ABCD中,BC∥AD,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2DC=2\sqrt{5}$.
如图,如图,在四棱锥S-ABCD中,底面梯形ABCD中,BC∥AD,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2DC=2\sqrt{5}$.