题目内容
19.已知函数F(x)=xf(x),f(x)满足f(x)=f(-x),且当x∈(-∞,0]时,F'(x)<0成立,若$a={2^{0.1}}•f({{2^{0.1}}}),b=ln2•f({ln2}),c={log_2}\frac{1}{8}•f({{{log}_2}\frac{1}{8}})$,则a,b,c的大小关系是( )| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | a>c>b |
分析 f(x)=f(-x),函数f(x)是偶函数,可得函数F(x)=xf(x)是奇函数.由当x∈(-∞,0]时,F'(x)<0成立,可得函数F(x)在x∈(-∞,0]时单调递减,因此函数F(x)在x∈R上单调递减.
解答 解:∵f(x)=f(-x),函数f(x)是偶函数,∴函数F(x)=xf(x)是奇函数.
∵当x∈(-∞,0]时,F'(x)<0成立,∴函数F(x)在x∈(-∞,0]时单调递减,
因此函数F(x)在x∈R上单调递减.
∵20.1>1,ln2∈(0,1),$lo{g}_{2}\frac{1}{8}$<0,$a={2^{0.1}}•f({{2^{0.1}}}),b=ln2•f({ln2}),c={log_2}\frac{1}{8}•f({{{log}_2}\frac{1}{8}})$,
∴a<b<c.
故选:C.
点评 本题考查了函数的奇偶性、单调性、指数函数与对数函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
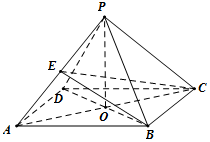 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.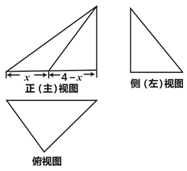 已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.
已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.