题目内容
12.已知函数f(x)=$\left\{\begin{array}{l}{1-x,x≤0}\\{(\frac{1}{2})^{x},x>0}\end{array}\right.$,若a=f(log3$\frac{1}{2}$),b=f(2${\;}^{-\frac{1}{2}}$),c=f(3${\;}^{\frac{1}{2}}$),则( )| A. | c>b>a | B. | c>a>b | C. | a>c>b | D. | a>b>c |
分析 由分段函数运用对数函数的单调性求出a>1,运用指数函数的单调性,判断0<c<b<1,进而得到a,b,c的大小.
解答 解:函数f(x)=$\left\{\begin{array}{l}{1-x,x≤0}\\{(\frac{1}{2})^{x},x>0}\end{array}\right.$,
则a=f(log3$\frac{1}{2}$)=1-log3$\frac{1}{2}$=1+log32>1,
b=f(2${\;}^{-\frac{1}{2}}$)=f($\frac{1}{\sqrt{2}}$)=2${\;}^{-\frac{1}{\sqrt{2}}}$∈(0,1),
c=f(3${\;}^{\frac{1}{2}}$)=2${\;}^{-\sqrt{3}}$∈(0,1),
由y=2x在R上递增,
-$\sqrt{3}$<-$\frac{1}{\sqrt{2}}$,可得2${\;}^{-\sqrt{3}}$<2${\;}^{-\frac{1}{\sqrt{2}}}$,
则c<b<a,
故选:D.
点评 本题考查分段函数的运用:比较函数值的大小,注意运用对数函数和指数函数的单调性,考查运算能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
3.定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}<0$.则( )
| A. | f(3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(3) | C. | f(-2)<f(1)<f(3) | D. | f(3)<f(1)<f(-2) |
7.集合A={x∈N+|-1<x<4},B={x|x2≤4},则A∩B=( )
| A. | {0,1,2} | B. | {1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
17.设函数f(x)是定义在R上的函数,满足f(x)=f(4-x),且对任意x1,x2∈(0,+∞),都有(x1-x2)[f(x1+2)-f(x2+2)]>0,则满足f(2-x)=f($\frac{3x+11}{x+4}$)的所有x的和为( )
| A. | -3 | B. | -5 | C. | -8 | D. | 8 |
1.已知一个圆锥的正视图和侧视图都是边长为1的正三角形,则它的俯视图的面积是( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
2.执行如图所示的程序框图,则输出的a值为( )
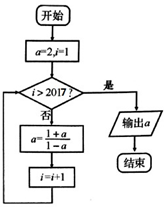

| A. | -3 | B. | $\frac{1}{3}$ | C. | $-\frac{1}{2}$ | D. | 2 |
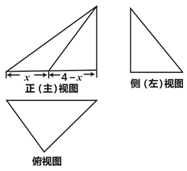 已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.
已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.