题目内容
函数f（x）=
的最大值是 ．
| 2 |
| 2-x(2-x) |
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：化简分式的分母，利用二次函数求出分母的最小值，即可求解函数的最大值．
解答：
解：函数f（x）=
=
，∵（x-1）2+1≥1，∴
≤2．
函数的最大值为2．
故答案为：2．
| 2 |
| 2-x(2-x) |
| 2 |
| (x-1)2+1 |
| 2 |
| (x-1)2+1 |
函数的最大值为2．
故答案为：2．
点评：本题考查函数的最值的求法，二次函数的性质的应用，考查计算能力．
练习册系列答案
相关题目
已知集合M={x|x=1+a2，a∈N*}，P={x|x=a2-2a+2，a∈N*}，则集合M与P的关系是（ ）
| A、M?P | B、P?M |
| C、M=P | D、M?P且P?M |
已知平面向量
=（1，1），
=（-1，1），则向量-2
-
的坐标是（ ）
| a |
| b |
| a |
| b |
| A、（-1，-3） |
| B、（-3，1） |
| C、（-1，0） |
| D、（-1，2） |
若集合M={-1，0，1，2}，N={1，0}，则M∪N=（ ）
| A、{0，1} |
| B、{-1，0，1，2} |
| C、{-1，0，1} |
| D、{0，1，2} |
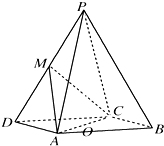如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠ADC=60°，AD=AM=1，PC=2，M为PD的中点．函数y=x3-2x2+2x共有（ ）个极值．
| A、0 | B、1 | C、2 | D、3 |