题目内容
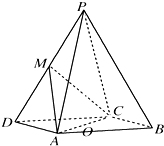 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ADC=60°,AD=AM=1,PC=2,M为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ADC=60°,AD=AM=1,PC=2,M为PD的中点.(1)证明PB∥平面ACM;
(2)求直线AM与直线PC所成角的余弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结AC,BD,交于点O,由已知得OM∥PB,由此能证明PB∥平面ACM.
(2)取CD中点N,连结MN,∠AMN是直线AM与直线PC所成的角,由此利用余弦定理能求出线AM与直线PC.
(2)取CD中点N,连结MN,∠AMN是直线AM与直线PC所成的角,由此利用余弦定理能求出线AM与直线PC.
解答:
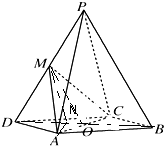 (1)证明:连结AC,BD,交于点O,
(1)证明:连结AC,BD,交于点O,
∵底面ABCD为菱形,∴O是BD中点,
连结OM,∵M为PD的中点,
∴OM∥PB,
∵OM?平面ACM,PB不包含于平面ACM,
∴PB∥平面ACM.
(2)解:取CD中点N,连结MN,
∵M是PD中点,∴MN∥PC,
∴∠AMN是直线AM与直线PC所成的角,
∵AM=AD=1,MN=
PC=1,
∠ADC=60°,AD=AM=1,
∴AN=
=
,
∴cos∠AMN=
=
,
∴直线AM与直线PC所成角的余弦值为
.
 (1)证明:连结AC,BD,交于点O,
(1)证明:连结AC,BD,交于点O,∵底面ABCD为菱形,∴O是BD中点,
连结OM,∵M为PD的中点,
∴OM∥PB,
∵OM?平面ACM,PB不包含于平面ACM,
∴PB∥平面ACM.
(2)解:取CD中点N,连结MN,
∵M是PD中点,∴MN∥PC,
∴∠AMN是直线AM与直线PC所成的角,
∵AM=AD=1,MN=
| 1 |
| 2 |
∠ADC=60°,AD=AM=1,
∴AN=
1+
|
| ||
| 2 |
∴cos∠AMN=
1+1-
| ||
| 2×1×1 |
| 5 |
| 8 |
∴直线AM与直线PC所成角的余弦值为
| 5 |
| 8 |
点评:本题考查直线与平面平行的证明,考查直线与直线所成角的余弦值的求法,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
已知f(x)=
,则f[f(0)]的值是( )
|
| A、0 | B、π |
| C、π2 | D、4 |
 如图,将等比数列{an}的前6项填入一个三角形的顶点及各边中点的位置,且在图中每个三角形的顶点所填的三项也成等比数列,数列{an}的前2013项和S2013=4026,则满足n
如图,将等比数列{an}的前6项填入一个三角形的顶点及各边中点的位置,且在图中每个三角形的顶点所填的三项也成等比数列,数列{an}的前2013项和S2013=4026,则满足n