题目内容
8.某封闭几何体的三视图如图所示,则该几何体的表面积为222+6$\sqrt{41}$
分析 由已知中的三视图可得该几何体是一个三棱柱切去一个三棱锥所得的组合体,画出直观图,计算各个面的面积,相加可得答案.
解答 解:由已知中的三视图可得该几何体是一个三棱柱切去一个三棱锥所得的组合体,
其直观图如图所示:
底面△ABC的面积为:$\frac{1}{2}$×8×6=24;
侧面ACDE的面积为:$\sqrt{{6}^{2}+{8}^{2}}$×10=100,
侧面ABFE的面积为:$\frac{1}{2}$(4+10)×6=42,
侧面CBFD的面积为:$\frac{1}{2}$(4+10)×8=56,
面EFD中,EF=6$\sqrt{2}$,FD=10,ED=10,
故面积为:$\frac{1}{2}$×6$\sqrt{2}$×$\sqrt{{10}^{2}-(\frac{6\sqrt{2}}{2})^{2}}$=6$\sqrt{41}$,
故几何体的表面积S=222+6$\sqrt{41}$,
故答案为:222+6$\sqrt{41}$
点评 本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
16.在长方体ABCD-A1B1C1D1中,E、F分别是棱BC,CC1上的点,CF=AB=2CE,AB:AD:AA1=1:2:4,二面角A1-ED-F的正弦值$\frac{\sqrt{5}}{3}$.
20.函数f(x)的定义域为R,且满足f(1)=2,f′(x)<1,则不等式f(x)<x+1的解集为( )
| A. | (1,+∞) | B. | (-∞,1) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
17.设a,b,c为非零实数,则x=$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{c}{|c|}$+$\frac{{|{abc}|}}{abc}$的所有值所组成的集合为( )
| A. | {0,4} | B. | {-4,0} | C. | {-4,0,4} | D. | {0} |
18.若函数f(x)=lnx+$\frac{a}{x}$在区间[1,e]上最小值为$\frac{3}{2}$,则实数a的值为( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{e}$ | C. | $\frac{e}{2}$ | D. | 非上述答案 |
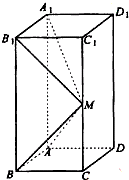 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,