题目内容
5.曲线f(x)=xex在点P(1,e)处的切线与坐标轴围成的三角形面积为$\frac{e}{4}$.分析 利用导数的几何意义求出切线方程,计算切线与坐标轴的交点坐标,即可得出三角形面积.
解答 解:f′(x)=ex+xex=ex(x+1),
∴切线斜率k=f′(1)=2e,
∴f(x)在(1,e)处的切线方程为y-e=2e(x-1),即y=2ex-e,
∵y=2ex-e与坐标轴交于(0,-e),($\frac{1}{2}$,0).
∴y=2ex-e与坐标轴围成的三角形面积为S=$\frac{1}{2}×e×\frac{1}{2}$=$\frac{e}{4}$.
故答案为:$\frac{e}{4}$.
点评 本题考查了导数的几何意义,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.若m<n<0,则下列不等式中正确的是( )
| A. | $\frac{1}{n}>\frac{1}{m}$ | B. | |n|>|m| | C. | $\frac{n}{m}+\frac{m}{n}>2$ | D. | m+n>mn |
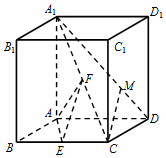 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.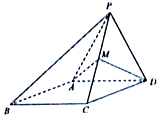 如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
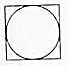
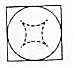
如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.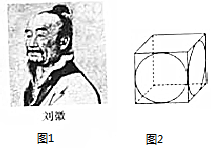 我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )
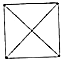
我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )
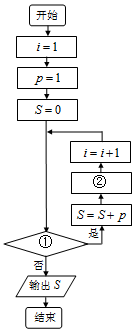 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.