Question

已知

1

m

+

2

n

=1(m＞0，n＞0)，当mn取得最小值时，直线y=-

2

x+2与曲线

x|x|

m

+

y|y|

n

=1交点个数为

2

．

Answer 1

分析：由均值不等式1=

1

m

+

2

n

≥2

1 m •  1 n

，当且仅当

1

m

=

2

n

时等号成立，所以m=2，n=4．故

x|x|

2

+

y|y|

4

=1．①当x＞0，y＞0，表示

x2

2

+ 

y2

4

=1的椭圆；②当x＞0，y＜0，表示

x2

2

- 

y2

4

=1以x轴为实轴的双曲线；③当x＜0，y＞0，表示

y2

4

-

x2

2

=1以y轴为实轴的双曲线；④当x＜0，y＜0，表示-

x2

2

-

y2

4

=1，因为左边恒≤0所以不可能=右边，所以此时无解．作出图象能得到结果．

解答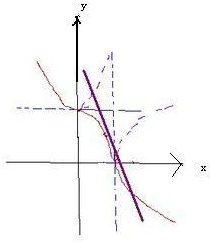：解：由均值不等式
1=

1

m

+

2

n

≥2

1 m •  1 n

，
当且仅当

1

m

=

2

n

时等号成立，
也就是

1

m

=

2

n

=

1

2

，
所以m=2，n=4．
∵

x|x|

m

+

y|y|

n

=1，
∴

x|x|

2

+

y|y|

4

=1．
①当x＞0，y＞0，
表示

x2

2

+ 

y2

4

=1的椭圆；
②当x＞0，y＜0，
表示

x2

2

- 

y2

4

=1以x轴为实轴的双曲线；
③当x＜0，y＞0，
表示

y2

4

-

x2

2

=1以y轴为实轴的双曲线；
④当x＜0，y＜0，
表示-

x2

2

-

y2

4

=1，
因为左边恒≤0所以不可能=右边，
所以此时无解．
所以如图得到图象，
结合图象知直线y=-

2

x+2与曲线

x|x|

m

+

y|y|

n

=1交点个数是2个．
故答案为：2．

点评：本题考查直线与圆锥曲线的综合应用，解题时要注意均值定理和分类讨论思想、数形结合思想的合理运用．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，常因分类不清易出错，是高考的重点．解题时要认真审题，仔细解答．