题目内容

已知函数f（x）=2sinxcosx+2cos2x-1（x∈R）
（1）求f（x）的最大值，并求使f（x）取最大值时x的集合；
（2）若θ为锐角，且f（θ+
π
8
）=
2
3
，求sin2θ的值．
考点：同角三角函数基本关系的运用
专题：三角函数的求值,三角函数的图像与性质
分析：（1）化简可得：f（x）=
2
sin（2x+
π
4
）．由2kπ+
π
2
=2x+
π
4
，k∈Z，可解得当x=kπ+
π
8
，k∈Z时，f（x）max=
2
．
（2）由f（θ+
π
8
）=
2
sin[2（θ+
π
8
）+
π
4
]=
2
3
，可得cos2θ=
1
3
，又θ为锐角，从而可求sin2θ=
1-cos2θ
=
2
2
3
．
解答： 解：（1）化简可得：f（x）=2sinxcosx+2cos2x-1=
2
sin（2x+
π
4
）．
所以有，2kπ+
π
2
=2x+
π
4
，k∈Z，可解得：当x=kπ+
π
8
，k∈Z时，f（x）max=
2
．
（2）∵f（θ+
π
8
）=
2
sin[2（θ+
π
8
）+
π
4
]=
2
3
，
∴整理化简可得：cos2θ=
1
3
，
∵θ为锐角，∴0＜2θ＜π
∴sin2θ=
1-cos2θ
=
2
2
3
．
点评：本题主要考察了同角三角函数基本关系的运用，三角函数的求值，属于基本知识的考查．
练习册系列答案
相关题目
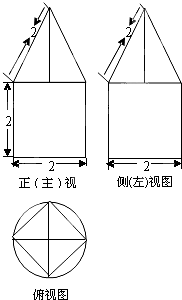在装有相同数量的白球和黑球的口袋中放进1个白球，此时由这个口袋中取出1个白球的概率比口袋中原来取出一个白球的概率大0.1，则口袋中原有球的个数是（　　）
A、2B、4C、8D、10
一空间几何体的三视图如图所示，则该几何体的表面积为（　　）
A、6π+4
2
-2
B、6π+4
2
C、2π+
2
3
3
D、2π+4
3
已知数列{an}满a1=
1
2
，an+1=an+
1
n2+n
，求an．
过抛物线y2=3x上一定点M（x0，y0）（y0＞0），作两条直线MA、MB分别交抛物线于A（x1，y1），B（x2，y2），当直线MA与MB的斜率存在且倾斜角互补时，
y1+y2
3y0
的值是（　　）
A、
1
3
B、
2
3
C、-3
D、-
2
3
给出下列结论：
①若
a
≠
0
，
a
•
b
=0，则
b
=
0
； 
②若
a
•
b
=
b
•
c
，则
a
=
c
；
③(
a
•
b
)
c
=
a
(
b
•
c
)；    
④
a
，
b
为非零不共线，若|
a
+
b
|=|
a
-
b
|，则
a
⊥
b
；
⑤
a
，
b
，
c
非零不共线，则(
b
•
c
)•
a
-(
c
•
a
)•
b
与
c
垂直
其中正确的为（　　）
A、②③B、①②④C、④⑤D、③④
不等式2x+4＜0的解集为
 
．
已知数列{an}的首项为1，向量
pn
=（1+an+1，-3），
qn
=（1，an+1），n∈N*，且
pn
⊥
qn
．
（1）求数列{an}的通项公式；
（2）数列{an}的前n项和．
函数y=
2x2-x+2
x2+x+1
的值域是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网