题目内容
已知函数f（x）=
，a∈R．则有f（x）的极大值为 ．
| 1-a+lnx |
| x |
考点：利用导数研究函数的极值
专题：导数的概念及应用
分析：先求出函数的导数，判断单调区间，找到极值点，从而求出函数的极大值．
解答：
解：∵f′（x）=
，（x＞0）
当f′（x）＞0时，解得：x＜ea，
当f（x）＜0时，解得：x＞ea，
∴x=ea时，函数f（x）取到极大值，
f（x）极大值=f（ea）=
=e-a，
故答案为：e-a．
| a-lnx |
| x2 |
当f′（x）＞0时，解得：x＜ea，
当f（x）＜0时，解得：x＞ea，
∴x=ea时，函数f（x）取到极大值，
f（x）极大值=f（ea）=
| 1-a+lnea |
| ea |
故答案为：e-a．
点评：本题考察了函数的单调性，函数的最值问题，导数的应用，是一道基础题．
练习册系列答案
相关题目
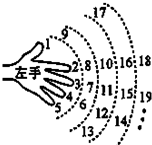如图，一个小朋友按如图所示的规则练习数数，1大拇指，2食指，3中指，4无名指，5小指，6无名指，…，一直数到2014时，对应的指头是