题目内容
设椭圆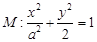
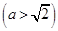 的右焦点为
的右焦点为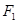 ,直线
,直线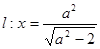 与
与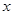 轴交于点
轴交于点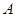 ,若
,若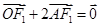 (其中
(其中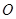 为坐标原点).
为坐标原点).
(I)求椭圆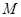 的方程;
的方程;
(II)设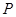 是椭圆
是椭圆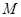 上的任意一点,
上的任意一点,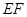 为圆
为圆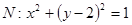 的任意一条直径(
的任意一条直径(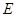 、
、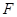 为直径的两个端点),求
为直径的两个端点),求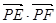 的最大值.
的最大值.
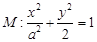
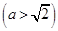 的右焦点为
的右焦点为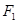 ,直线
,直线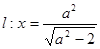 与
与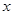 轴交于点
轴交于点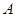 ,若
,若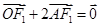 (其中
(其中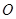 为坐标原点).
为坐标原点).(I)求椭圆
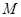 的方程;
的方程;(II)设
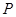 是椭圆
是椭圆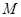 上的任意一点,
上的任意一点,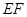 为圆
为圆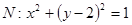 的任意一条直径(
的任意一条直径(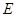 、
、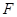 为直径的两个端点),求
为直径的两个端点),求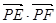 的最大值.
的最大值.(I)椭圆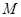 的方程为
的方程为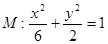 ;
;
(II)当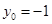 时,
时,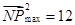 ,故
,故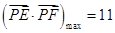
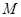 的方程为
的方程为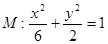 ;
;(II)当
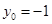 时,
时,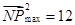 ,故
,故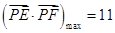
试题分析:(I)由题设知,
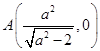 ,
,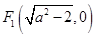 , 由
, 由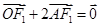 ,
,得
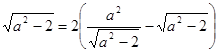 .解得
.解得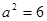 .所以椭圆
.所以椭圆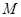 的方程为
的方程为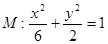
(II)方法1:设点
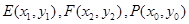 ,因为
,因为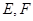 的中点坐标为
的中点坐标为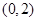 ,
,所以
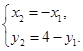 所以
所以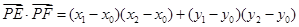
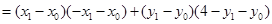
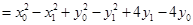
 .
.因为点
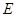 在圆
在圆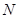 上,所以
上,所以 ,即
,即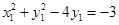 .
.因为点
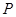 在椭圆
在椭圆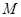 上,所以
上,所以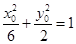 ,即
,即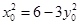 .
.故
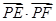
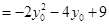
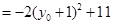 .
.因为
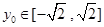 ,所以当
,所以当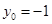 时,
时,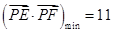
法2:由题知圆N:
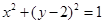 的圆心为N;则
的圆心为N;则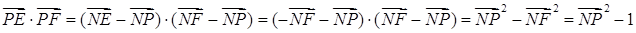
从而求
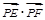 的最大值转化为求
的最大值转化为求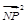 的最大值;
的最大值;因为点
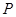 在椭圆
在椭圆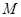 上,设点
上,设点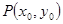 所以
所以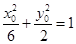 ,即
,即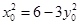 .
.又因为
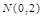 ,所以
,所以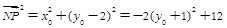 ;
;因为
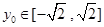 ,所以当
,所以当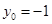 时,
时,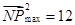 ,故
,故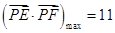
方法3:①若直线
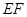 的斜率存在,设
的斜率存在,设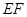 的方程为
的方程为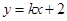 ,
, 由
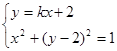 ,解得
,解得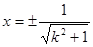 .因为
.因为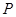 是椭圆
是椭圆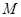 上的任一点,设点
上的任一点,设点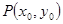 ,
,所以
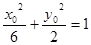 ,即
,即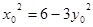 .所以
.所以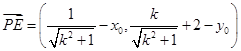
故
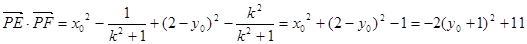 .
.因为
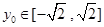 ,所以当
,所以当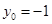 时,
时,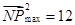 ,故
,故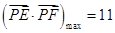
②若直线EF的斜率不存在,此时EF的方程为
 ; 由
; 由 ,解得
,解得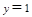 或
或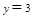 .
. 不妨设E(0,3),F(0,1); 因为点
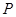 在椭圆
在椭圆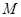 上,设点
上,设点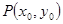 所以
所以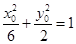 ,即
,即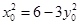
所以
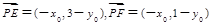 ,故
,故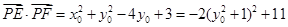
因为
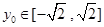 ,所以当
,所以当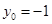 时,
时,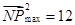 ,故
,故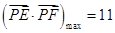
点评:难题,求椭圆的标准方程,主要运用了椭圆的几何性质,注意明确焦点轴和a,b,c的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)注意讨论直线的斜率存在、不存在两种情况,易于忽视。熟练进行平面向量的坐标运算,是正确解题的关键。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
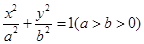 过点
过点 ,其长轴、焦距和短轴的长的平方依次成等差数列.
,其长轴、焦距和短轴的长的平方依次成等差数列. 轴正半轴、
轴正半轴、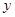 轴分别交于点
轴分别交于点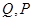 ,与椭圆分别交于点
,与椭圆分别交于点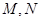 ,各点均不重合,且满足
,各点均不重合,且满足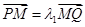 ,
,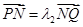 . 当
. 当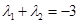 时,试证明直线过定点.过定点(1,0)
时,试证明直线过定点.过定点(1,0)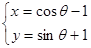 ,(
,(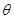 为参数)的普通方程为 ( )
为参数)的普通方程为 ( )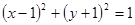
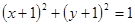
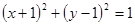

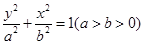 的上、下焦点,其中F1也是抛物线C2:
的上、下焦点,其中F1也是抛物线C2: 的焦点,点A是曲线C1,C2在第二象限的交点,且
的焦点,点A是曲线C1,C2在第二象限的交点,且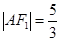

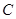 1的方程;
1的方程;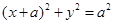 的直径,求
的直径,求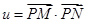 的最大值和最小值.
的最大值和最小值.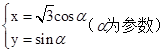 .
. ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;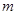 ,
,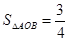 ;
;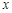 轴上的椭圆C,其长轴长等于4,离心率为
轴上的椭圆C,其长轴长等于4,离心率为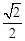 .
.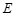 (0,1), 问是否存在直线
(0,1), 问是否存在直线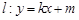 与椭圆
与椭圆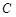 交于
交于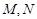 两点,且
两点,且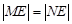 ?若存在,求出
?若存在,求出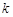 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.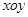 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线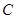 的极坐标方程为
的极坐标方程为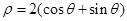 .
.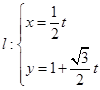 (
(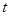 为参数)与曲线C交于
为参数)与曲线C交于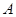 ,
,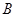 两点,与
两点,与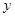 轴交于
轴交于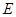 ,求
,求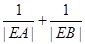 的值.
的值.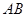 是过抛物线
是过抛物线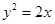 焦点的弦,
焦点的弦,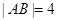 ,则
,则