题目内容
已知中心在坐标原点焦点在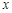 轴上的椭圆C,其长轴长等于4,离心率为
轴上的椭圆C,其长轴长等于4,离心率为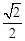 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点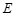 (0,1), 问是否存在直线
(0,1), 问是否存在直线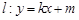 与椭圆
与椭圆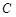 交于
交于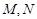 两点,且
两点,且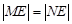 ?若存在,求出
?若存在,求出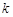 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
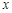 轴上的椭圆C,其长轴长等于4,离心率为
轴上的椭圆C,其长轴长等于4,离心率为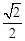 .
.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点
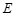 (0,1), 问是否存在直线
(0,1), 问是否存在直线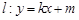 与椭圆
与椭圆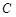 交于
交于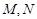 两点,且
两点,且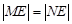 ?若存在,求出
?若存在,求出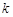 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.(Ⅰ) 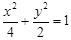 (Ⅱ) 存在这样的直线
(Ⅱ) 存在这样的直线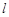 ,其斜率
,其斜率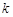 的取值范围是
的取值范围是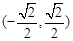
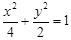 (Ⅱ) 存在这样的直线
(Ⅱ) 存在这样的直线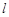 ,其斜率
,其斜率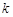 的取值范围是
的取值范围是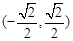
试题分析:(Ⅰ)由题意可设椭圆的标准方程为
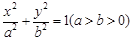 1分
1分则由长轴长等于4,即2a=4,所以a=2. 2分
又
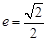 ,所以
,所以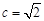 , 3分
, 3分又由于
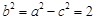 4分
4分所求椭圆C的标准方程为
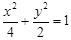 5分
5分(Ⅱ)假设存在这样的直线
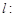
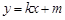 ,设
,设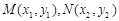 ,
,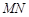 的中点为
的中点为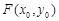
因为
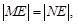 所以
所以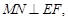 所以
所以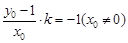 ①
①(i)其中若
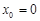 时,则
时,则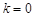 ,显然直线
,显然直线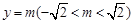 符合题意;
符合题意;(ii)下面仅考虑
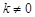 情形:
情形:由
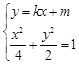 ,得
,得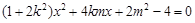 ,
,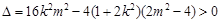 ,得
,得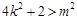 ② 7分
② 7分则
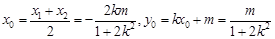 . 8分
. 8分代入①式得,即
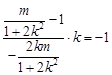 ,解得
,解得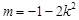 11分
11分代入②式得
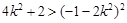 ,得
,得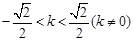 .
.综上(i)(ii)可知,存在这样的直线
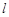 ,其斜率
,其斜率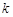 的取值范围是
的取值范围是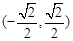 13分
13分点评:直线与椭圆相交时常将直线与椭圆联立方程组,利用韦达定理找到根与系数的关系,进而将
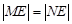 转化为点的坐标表示,其中要注意条件
转化为点的坐标表示,其中要注意条件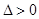 不要忽略
不要忽略
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 的离心率为
的离心率为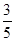 ,两焦点分别为
,两焦点分别为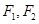 ,点M是椭圆C上一点,
,点M是椭圆C上一点,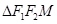 的周长为16,设线段MO(O为坐标原点)与圆
的周长为16,设线段MO(O为坐标原点)与圆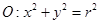 交于点N,且线段MN长度的最小值为
交于点N,且线段MN长度的最小值为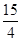 .
.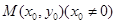 在椭圆C上运动时,判断直线
在椭圆C上运动时,判断直线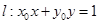 与圆O的位置关系.
与圆O的位置关系.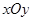 中,点
中,点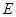 到两点
到两点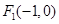 ,
,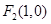 的距离之和为
的距离之和为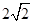 ,设点
,设点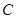 .
.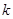 (
(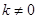 )的直线
)的直线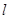 与曲线
与曲线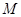 ,
,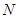 ,点
,点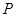 在
在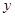 轴上,且
轴上,且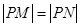 ,求点
,求点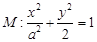
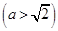 的右焦点为
的右焦点为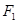 ,直线
,直线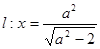 与
与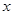 轴交于点
轴交于点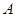 ,若
,若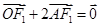 (其中
(其中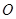 为坐标原点).
为坐标原点).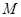 的方程;
的方程;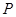 是椭圆
是椭圆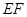 为圆
为圆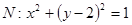 的任意一条直径(
的任意一条直径(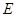 、
、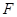 为直径的两个端点),求
为直径的两个端点),求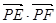 的最大值.
的最大值.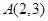 关于直线
关于直线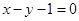 的对称点
的对称点 的坐标为 ;
的坐标为 ;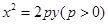 ,直线
,直线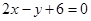 截抛物线C所得弦长为
截抛物线C所得弦长为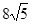 .
.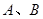 是抛物线上异于原点
是抛物线上异于原点 的两个动点,记
的两个动点,记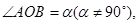 若
若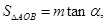 试求当
试求当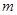 取得最小值时
取得最小值时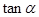 的最大值.
的最大值.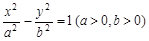 左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )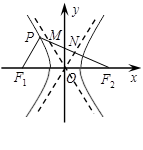

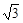

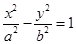 (
(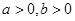 )的右焦点
)的右焦点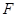 作圆
作圆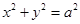 的切线
的切线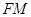 ,交
,交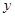 轴于点
轴于点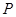 ,切圆于点
,切圆于点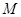 ,若
,若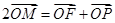 ,则双曲线的离心率是( )
,则双曲线的离心率是( )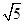
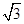
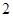
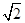
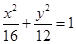 上找一点,使这一点到直线
上找一点,使这一点到直线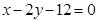 的距离为最小,并求最小值。
的距离为最小,并求最小值。