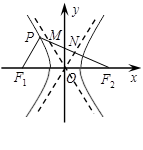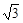题目内容
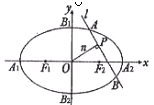
如图,已知F1、F2分别为椭圆C1: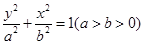 的上、下焦点,其中F1也是抛物线C2:
的上、下焦点,其中F1也是抛物线C2: 的焦点,点A是曲线C1,C2在第二象限的交点,且
的焦点,点A是曲线C1,C2在第二象限的交点,且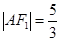

(Ⅰ)求椭圆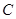 1的方程;
1的方程;
(Ⅱ)已知P是椭圆C1上的动点,MN是圆C: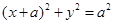 的直径,求
的直径,求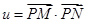 的最大值和最小值.
的最大值和最小值.
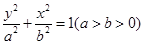 的上、下焦点,其中F1也是抛物线C2:
的上、下焦点,其中F1也是抛物线C2: 的焦点,点A是曲线C1,C2在第二象限的交点,且
的焦点,点A是曲线C1,C2在第二象限的交点,且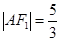

(Ⅰ)求椭圆
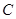 1的方程;
1的方程;(Ⅱ)已知P是椭圆C1上的动点,MN是圆C:
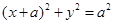 的直径,求
的直径,求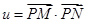 的最大值和最小值.
的最大值和最小值.(Ⅰ)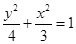 ;
;
(Ⅱ)当 时,
时,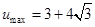 ,当
,当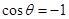 时,
时,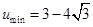 。
。
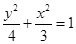 ;
;(Ⅱ)当
 时,
时,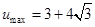 ,当
,当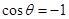 时,
时,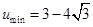 。
。试题分析:(Ⅰ)抛物线C2的焦点F1(0,1),准线
 ,易得
,易得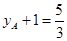 ∴
∴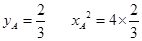
∴
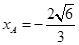 (正值舍去)∴
(正值舍去)∴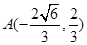 3分
3分又
 ………①
………① 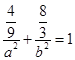 …………② 5分
…………② 5分联立①②得
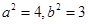 ∴椭圆C1的方程为
∴椭圆C1的方程为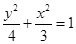 6分
6分(Ⅱ)圆C:
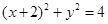 ∴圆心C(-2,0),半径
∴圆心C(-2,0),半径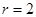
设P(
 ) 7分
) 7分法一:
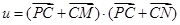 9分
9分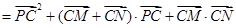
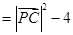
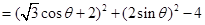
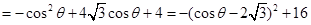 11分
11分当
 时,
时,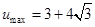 12分
12分当
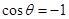 时,
时,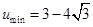 13分
13分法二:设M(
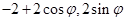 ),则N(
),则N(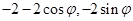 ) 8分
) 8分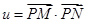
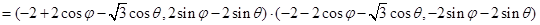
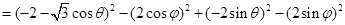
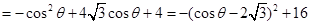 11分
11分当
 时,
时,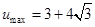 12分
12分当
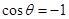 时,
时,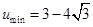 13分
13分法三:
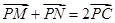 8分
8分
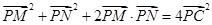
∵C是MN中点,∴
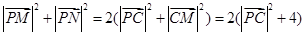 9分
9分∴
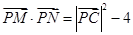 10分
10分∴
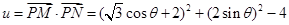
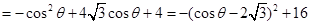 11分
11分当
 时,
时,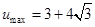 12分
12分当
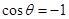 时,
时,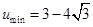 13分
13分点评:中档题,求椭圆的标准方程,主要运用了椭圆的几何性质,a,b,c,e的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)利用平面向量的坐标运算,将问题转化成三角函数问题,确定最值。

练习册系列答案
相关题目
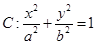 的顶点为
的顶点为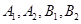 ,焦点为
,焦点为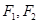 ,
,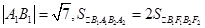 .
. 
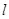 是与n垂直相交于P点,与椭圆相交于A, B两点的直线,
是与n垂直相交于P点,与椭圆相交于A, B两点的直线,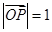 .是否存在上述直线
.是否存在上述直线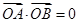 成立?若存在,求出直线
成立?若存在,求出直线 且与抛物线
且与抛物线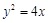 只有一个公共点的直线有( ).
只有一个公共点的直线有( ). 条
条 条
条 条
条 条
条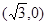
 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且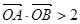 (其中O为原点). 求k的取值范围.
(其中O为原点). 求k的取值范围.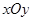 中,点
中,点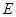 到两点
到两点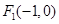 ,
,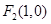 的距离之和为
的距离之和为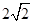 ,设点
,设点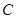 .
.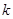 (
(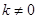 )的直线
)的直线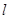 与曲线
与曲线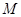 ,
,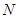 ,点
,点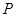 在
在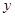 轴上,且
轴上,且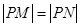 ,求点
,求点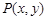 在椭圆
在椭圆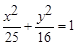 上,若
上,若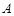 点坐标为
点坐标为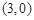 ,
,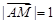 ,且
,且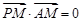 ,则
,则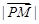 的最小值是( )
的最小值是( )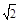
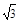
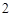

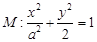
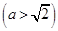 的右焦点为
的右焦点为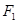 ,直线
,直线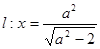 与
与 轴交于点
轴交于点 ,若
,若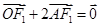 (其中
(其中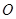 为坐标原点).
为坐标原点).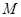 的方程;
的方程;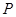 是椭圆
是椭圆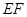 为圆
为圆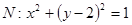 的任意一条直径(
的任意一条直径(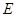 、
、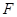 为直径的两个端点),求
为直径的两个端点),求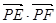 的最大值.
的最大值.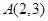 关于直线
关于直线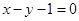 的对称点
的对称点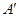 的坐标为 ;
的坐标为 ;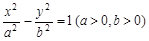 左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )