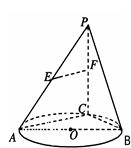
题目内容
如图,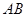 是圆
是圆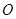 的直径,点
的直径,点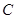 是圆
是圆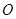 上异于
上异于 的点,直线
的点,直线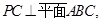
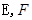 分别为
分别为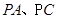 的中点。
的中点。
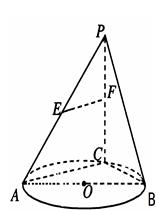
(1)记平面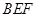 与平面
与平面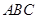 的交线为
的交线为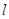 ,试判断
,试判断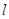 与平面
与平面 的位置关系,并加以说明;
的位置关系,并加以说明;
(2)设(1)中的直线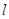 与圆
与圆 的另一个交点为
的另一个交点为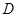 ,且点
,且点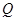 满足
满足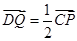 ,记直线
,记直线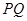
平面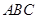 所成的角为
所成的角为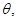 异面直线
异面直线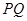 与
与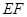 所成的锐角为
所成的锐角为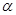 ,二面角
,二面角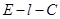 的大小为
的大小为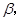
①求证: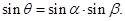
②当点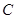 为弧
为弧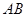 的中点时,
的中点时,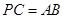 ,求直线
,求直线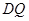 与平面
与平面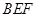 所成的角的正弦值。
所成的角的正弦值。
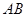 是圆
是圆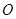 的直径,点
的直径,点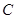 是圆
是圆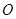 上异于
上异于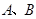 的点,直线
的点,直线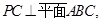
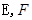 分别为
分别为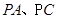 的中点。
的中点。
(1)记平面
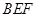 与平面
与平面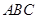 的交线为
的交线为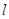 ,试判断
,试判断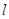 与平面
与平面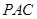 的位置关系,并加以说明;
的位置关系,并加以说明;(2)设(1)中的直线
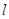 与圆
与圆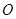 的另一个交点为
的另一个交点为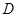 ,且点
,且点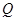 满足
满足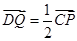 ,记直线
,记直线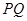
平面
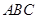 所成的角为
所成的角为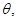 异面直线
异面直线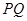 与
与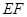 所成的锐角为
所成的锐角为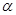 ,二面角
,二面角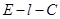 的大小为
的大小为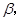
①求证:
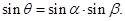
②当点
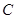 为弧
为弧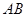 的中点时,
的中点时,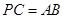 ,求直线
,求直线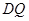 与平面
与平面 所成的角的正弦值。
所成的角的正弦值。(1)直线 ∥平面
∥平面 (2)①详见解析②
(2)①详见解析②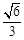
 ∥平面
∥平面 (2)①详见解析②
(2)①详见解析②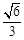
试题分析:(1)
 面
面 ,根据线线平行,线面平行,线与交线平行,
,根据线线平行,线面平行,线与交线平行,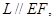 从而得出线面平行,(2)①连接
从而得出线面平行,(2)①连接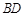 ,由( 1)可知交线
,由( 1)可知交线 即为直线
即为直线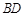 ,且
,且 ∥
∥ . 因为
. 因为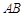 是
是 的直径,所以
的直径,所以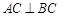 ,于是
,于是 .已知
.已知 平面
平面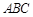 ,而
,而 平面
平面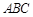 ,所以
,所以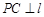 .而
.而 ,所以
,所以 平面
平面 ,在不同的直角三角形内构造
,在不同的直角三角形内构造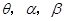 ,做出
,做出 .③因为
.③因为 ∥
∥ ,所以直线
,所以直线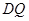 与平面
与平面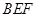 所成的角就为CF与平面
所成的角就为CF与平面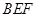 所成的角过点C作CG⊥BF,垂足为G,
所成的角过点C作CG⊥BF,垂足为G, 就是直线
就是直线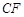 与平面
与平面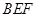 所成的角.
所成的角.试题解析:
解(1)直线
 ∥平面
∥平面 ,证明如下:连接
,证明如下:连接 ,因为
,因为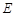 ,
, 分别是
分别是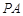 ,
,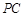 的中点,所以
的中点,所以 ∥
∥ . 又
. 又 平面
平面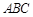 ,且
,且 平面
平面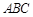 ,所以
,所以 ∥平面
∥平面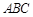 .而
.而 平面
平面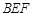 ,且平面
,且平面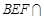 平面
平面 ,所以
,所以 ∥
∥ . 因为
. 因为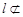 平面
平面 ,
, 平面
平面 ,所以直线
,所以直线 ∥平面
∥平面
(2)①证明:如图,
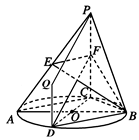
连接
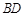 ,由(1)可知交线
,由(1)可知交线 即为直线
即为直线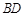 ,且
,且 ∥
∥ . 因为
. 因为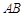 是
是 的直径,所以
的直径,所以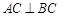 ,于是
,于是 .
.已知
 平面
平面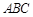 ,而
,而 平面
平面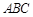 ,所以
,所以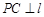 .而
.而 ,所以
,所以 平面
平面 .连接
.连接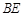 ,
,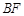 ,因为
,因为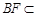 平面
平面 ,所以
,所以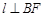 .故
.故 就是二面角
就是二面角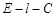 的平面角,即
的平面角,即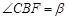 . 由
. 由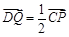 ,作
,作 ∥
∥ ,且
,且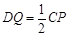 . 连接
. 连接 ,
,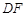 ,因为
,因为 是
是 的中点,
的中点, ,所以
,所以 ,
,从而四边形
 是平行四边形,
是平行四边形, ∥
∥ .连接
.连接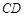 ,因为
,因为 平面
平面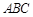 ,所以
,所以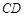 是
是 在平面
在平面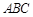 内的射影,故
内的射影,故 就是直线
就是直线 与平面
与平面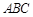 所成的角,即
所成的角,即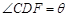 . 又
. 又 平面
平面 ,有
,有 ,知
,知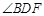 为锐角,故
为锐角,故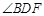 为异面直线
为异面直线 与
与 所成的角,即
所成的角,即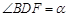 , 8分
, 8分于是在
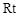 △
△ ,
,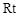 △
△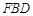 ,
,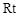 △
△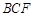 中,分别可得
中,分别可得 ,
,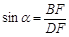 ,
, ,
,从而
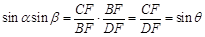 ,即
,即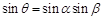 . 9分
. 9分②因为
 ∥
∥ ,所以直线
,所以直线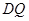 与平面
与平面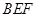 所成的角就为CF与平面
所成的角就为CF与平面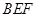 所成的角
所成的角过点C作CG⊥BF,垂足为G,因为
 平面
平面 所以
所以 CG,又
CG,又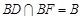 所以CG⊥平面
所以CG⊥平面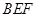
故
 就是直线
就是直线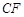 与平面
与平面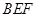 所成的角,
所成的角,  ,故直线
,故直线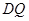 与平面
与平面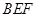 所成的角的正弦值为
所成的角的正弦值为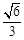 13分
13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 关于直线
关于直线 对称,
对称,
 .把
.把 沿
沿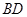 折起(如图二),使二面角
折起(如图二),使二面角 的余弦值等于
的余弦值等于 .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
 两点间的距离;
两点间的距离; 平面
平面 ;
; 所成角的正弦值.
所成角的正弦值.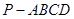 中,
中,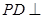 平面
平面 ,底面
,底面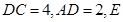 为
为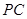 的中点.
的中点.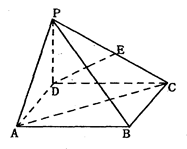
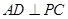 ;
;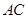 上是否存在一点
上是否存在一点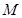 ,使得
,使得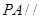 平面
平面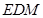 ?若存在,求出
?若存在,求出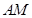 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.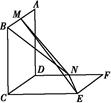
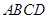 沿对角线
沿对角线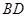 折成直二面角
折成直二面角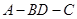 ,有如下四个结论:
,有如下四个结论: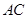 ⊥
⊥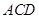 是等边三角形;③
是等边三角形;③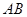 与平面
与平面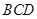 所成的角为60°;
所成的角为60°;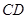 所成的角为60°.其中错误的结论是
所成的角为60°.其中错误的结论是 是直线,
是直线, 、
、 是两个不同的平面,则( )
是两个不同的平面,则( ) ,
,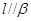 ,则
,则
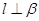 ,则
,则
 ,则
,则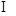 β;②a∥γ,b∥β;③b∥β,a
β;②a∥γ,b∥β;③b∥β,a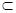 γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填序号).
γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填序号).