题目内容
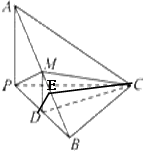
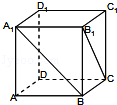
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
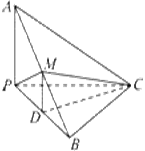
(1)求证DM∥平面APC;
(2)求证平面ABC⊥平面APC;
(3)若BC=PC=4,求二面角P-AB-C的正弦值.

(1)求证DM∥平面APC;
(2)求证平面ABC⊥平面APC;
(3)若BC=PC=4,求二面角P-AB-C的正弦值.
(3)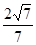
试题分析:
(1)从平面
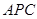 内找一条与
内找一条与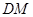 平行的直线,根据题意可知,
平行的直线,根据题意可知, 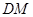 是
是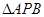 的中位线,有
的中位线,有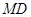 ∥
∥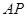 ,则证明.
,则证明.(2)要证面面垂直得有线面垂直,根据题意可证
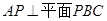 ,从而得到
,从而得到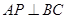 ,进而有
,进而有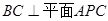 ,最终可证
,最终可证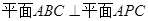 .
.(3)首先得做出二面角的平面角,所以过
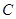 作
作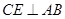 ,垂足为
,垂足为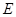 ,连接
,连接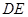 ,猜想
,猜想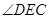 为二面角
为二面角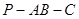 的平面角,根据二面角的平面角定义,只需证明
的平面角,根据二面角的平面角定义,只需证明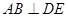 ,显然根据已知以及(1)中的结论,可证
,显然根据已知以及(1)中的结论,可证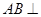 平面
平面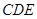 ,则可证明猜想.将
,则可证明猜想.将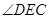 放入
放入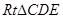 中,即可求其正弦值.
中,即可求其正弦值.证明
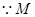 为
为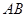 中点,
中点, 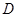 为
为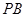 中点,
中点, 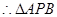 中,有
中,有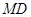 ∥
∥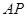 ,
,又
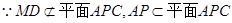 ,
, 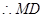 ∥平面
∥平面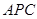
(2)证明
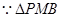 为正三角形,且
为正三角形,且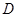 为
为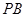 中点,
中点, 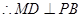
又由(1)知,
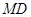 ∥
∥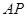 .
.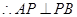
又
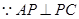 ,
, 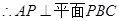
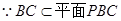
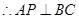
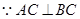
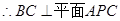
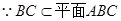
(3)
过
 作
作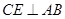 ,垂足为
,垂足为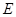 ,连接
,连接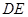 ,
, 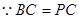 ,
,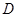 为
为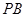 中点,
中点,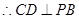 ,又由(2)知
,又由(2)知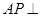 平面
平面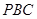 ,
,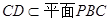
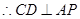 ,
,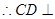 平面
平面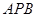 ,
,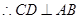
又
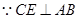
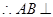 平面
平面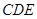 ,
,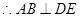
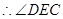 为二面角
为二面角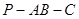 的平面角
的平面角 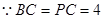 ,
,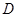 为
为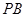 中点,,又由(2)
中点,,又由(2)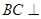 平面
平面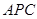 ,∴
,∴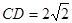 ,
,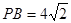 ,
,又
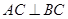 ,
,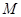 为
为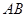 中点,
中点,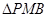 为正三角形,
为正三角形,∴
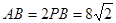 ,
,∴
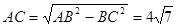 ,
,∴
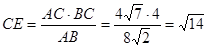
∴在
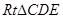 ,
,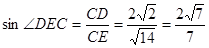
即二面角
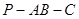 的正弦值为
的正弦值为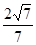 .
. 
练习册系列答案
相关题目

 ,
, ,
, ,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转
,N是BC的中点.如图所示,将梯形ABCD绕AB逆时针旋转 ,得到梯形
,得到梯形 .
.
 平面
平面 ;
;  平面
平面 ;
; 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形, ∥
∥ ,
, ,
, ,
, .
. 平面
平面 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.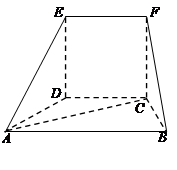
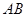 是圆
是圆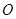 的直径,点
的直径,点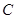 是圆
是圆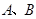 的点,直线
的点,直线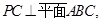
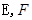 分别为
分别为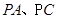 的中点。
的中点。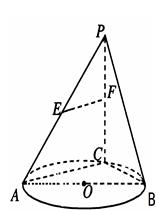
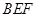 与平面
与平面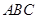 的交线为
的交线为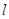 ,试判断
,试判断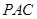 的位置关系,并加以说明;
的位置关系,并加以说明;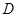 ,且点
,且点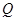 满足
满足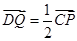 ,记直线
,记直线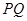
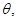 异面直线
异面直线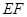 所成的锐角为
所成的锐角为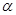 ,二面角
,二面角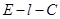 的大小为
的大小为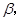
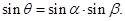
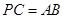 ,求直线
,求直线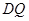 与平面
与平面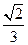
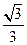
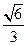
 的侧棱
的侧棱 在下底面的射影
在下底面的射影 与
与 平行,若
平行,若 ,且
,且 ,则
,则 的余弦值为( )
的余弦值为( )



