Question

9．如图是函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜2π）在一个周期内的图象，则（　　）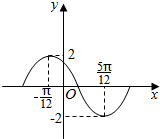

• A． A=2，ω=2，φ=$\frac{π}{3}$
• B． A=2，ω=2，φ=$\frac{2π}{3}$
• C． A=2，ω=$\frac{1}{2}$，φ=-$\frac{π}{3}$
• D． A=2，ω=2，φ=-$\frac{π}{3}$

Answer 1

分析 由图象易得A值，由周期公式可得ω，代点结合角的范围可得φ值．

解答 解：由图象可得A=2，周期T=$\frac{2π}{ω}$=2[$\frac{5π}{12}$-（-$\frac{π}{12}$）]，解得ω=2，
∴y=2sin（2x+φ），代点（-$\frac{π}{12}$，2）可得2=2sin（-$\frac{π}{6}$+φ），
∴sin（-$\frac{π}{6}$+φ）=1，∴-$\frac{π}{6}$+φ=2kπ+$\frac{π}{2}$，
解得φ=2kπ+$\frac{2π}{3}$，k∈Z，结合0＜φ＜2π可得φ=$\frac{2π}{3}$
故选：B

点评 本题考查三角函数的图象和解析式，属基础题．