若sinA-cosA=$\frac{\sqrt{5}}{2}$.则sinA•cosA的值为-$\frac{1}{8}$．题目和参考答案——青夏教育精英家教网——

题目内容

14．若sinA-cosA=$\frac{\sqrt{5}}{2}$，则sinA•cosA的值为-$\frac{1}{8}$．

分析由条件利用同角三角函数的基本关系，求得sinA•cosA的值．

解答解：∵sinA-cosA=$\frac{\sqrt{5}}{2}$，则平方可得1-2sinA•cosA=$\frac{5}{4}$，
求得sinAcosA=-$\frac{1}{8}$，
故答案为：-$\frac{1}{8}$．

点评本题主要考查同角三角函数的基本关系，属于基础题．

练习册系列答案

周报经典英语周报系列答案

假期作业吉林教育出版社系列答案

口算题天天练系列答案

正大图书练测考系列答案

一本必胜系列答案

进阶集训系列答案

尖子生单元测试系列答案

轻松假期行暑假用书系列答案

世纪百通主体课堂小学课时同步练习系列答案

经纶学典棒棒堂系列答案

相关题目

2．将函数y=sin（ωx-$\frac{π}{6}$）（ω＞0）的图象向左平移$\frac{π}{3ω}$个单位，得到函数f（x）的图象，若函数f（x）在（0，2]上恰有一个最大值1和最小值-1，则ω的取值范围是$\frac{2π}{3}$≤ω＜$\frac{7π}{6}$．

5．圆心为（-3，2）且过点A（1，-1）的圆的方程是（　　）

（x-3）²+（y-2）²=5

（x+3）²+（y-2）²=5

（x-3）²+（y-2）²=25

（x+3）²+（y-2）²=25

2．已知角α的顶点与直角坐标系的原点重合，始边与x轴的非负半轴重合，若点P（1，-$\sqrt{3}$）是角α终边上一点，则tanα的值为（　　）

-$\frac{\sqrt{3}}{2}$

-$\frac{\sqrt{3}}{2}$

9．如图是函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜2π）在一个周期内的图象，则（　　）

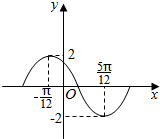
A=2，ω=2，φ=$\frac{π}{3}$

A=2，ω=2，φ=$\frac{2π}{3}$

A=2，ω=$\frac{1}{2}$，φ=-$\frac{π}{3}$

A=2，ω=2，φ=-$\frac{π}{3}$

19．已知sin（α+$\frac{π}{8}$）cos（α+$\frac{π}{8}$）=$\frac{\sqrt{3}}{4}$，α∈（$\frac{π}{8}$，$\frac{π}{4}$），cos（2β-$\frac{π}{4}$）=$\frac{3}{5}$，β∈（$\frac{π}{4}$，$\frac{π}{2}$）．
（1）求sin（2α+$\frac{π}{4}$）及cos（2α+$\frac{π}{4}$）的值；
（2）求cos（2α+2β）的值．

6．在一次模拟考试后，从高三某班随机抽取了20位学生的数学成绩，其分布如下：

分组	[90，100]	[100，110）	[110，120）	[120，130）	[130，140）	[140，150）
频数	1	2	6	7	3	1

分数在130分（包括130分）以上者为优秀，据此估计该班的优秀率约为（　　）

有一个容量为n的样本，其频率分布直方图如图所示，已知样本数据在区间[10，12）内的频数为18，则实数n=100．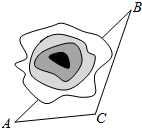

如图，在铁路建设中需要确定隧道的长度和隧道两端的施工方向，已测得隧道两端的两点A，B到某一点C的距离分别为2千米，2$\sqrt{3}$千米及∠ACB=150°，则A，B两点间的距离为2$\sqrt{7}$千米．