题目内容
20.若函数f(x)的定义域是[0,4],则函数f(2x-3)的定义域是$[{\frac{3}{2},\frac{7}{2}}]$.分析 由已知函数的定义域,可得0≤2x-3≤4,解此不等式得答案.
解答 解:∵函数f(x)的定义域是[0,4],
则由0≤2x-3≤4,得$\frac{3}{2}≤x≤\frac{7}{2}$,
∴函数f(2x-3)的定义域是$[{\frac{3}{2},\frac{7}{2}}]$.
故答案为:$[{\frac{3}{2},\frac{7}{2}}]$.
点评 本题考查函数的定义域及其求法,关键是掌握该类问题的求解方法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若二次函数y=ax2+bx+c的图象不过第四象限且对称轴在y轴左边那么a,b,c的取值可以为( )
| A. | a>0,b>0,c≥0. | B. | a>0,b<0,c≤0 | C. | a<0,b>0,c≥0 | D. | a<0,b<0,c≤0 |
15.如图,在四面体ABCD中,设G是CD的中点,则$\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BD}+\overrightarrow{BC})$等于( )
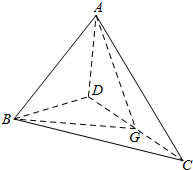

| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{BG}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{AG}$ |
5.圆心为(-3,2)且过点A(1,-1)的圆的方程是( )
| A. | (x-3)2+(y-2)2=5 | B. | (x+3)2+(y-2)2=5 | C. | (x-3)2+(y-2)2=25 | D. | (x+3)2+(y-2)2=25 |
9.如图是函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)在一个周期内的图象,则( )
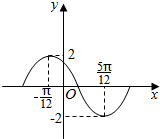

| A. | A=2,ω=2,φ=$\frac{π}{3}$ | B. | A=2,ω=2,φ=$\frac{2π}{3}$ | C. | A=2,ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ | D. | A=2,ω=2,φ=-$\frac{π}{3}$ |
10.某校羽毛球小组有男学生A,B,C和女学生X,Y,Z共6人,其所属年级如下:
现从这6名学生中随机选出2人参加羽毛球比赛(每人被选到的可能性相同).
(1)共有几种不同的选法?用表中字母列举出来;
(2)设M为事件“选出的2人性别相同”,求事件M发生的概率.
| 一年级 | 二年级 | 三年级 | |
| 男生 | A | B | C |
| 女生 | X | Y | Z |
(1)共有几种不同的选法?用表中字母列举出来;
(2)设M为事件“选出的2人性别相同”,求事件M发生的概率.
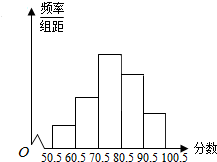 从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.
从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.