题目内容
18．
已知甲、乙两组数据如茎叶图所示，若它们的中位数相同，平均数也相同，则图中m与n的乘积mn=（ ）| A． | 12 | B． | 16 | C． | 18 | D． | 24 |
分析 根据茎叶图中中位数相同，平均数也相同确定m，n的值即可得到结论．
解答 解：乙的中位数为$\frac{1}{2}$（32+34）=33，
则甲的中位数为33，即m=3，
甲的平均数为$\frac{1}{3}$（27+33+39）=33，
则乙的平均数为$\frac{1}{4}$（20+n+32+34+38）=33，
解得n=8，
∴mn=24，
故选：D．
点评 本题主要考查茎叶图，中位数和平均数的概念和计算，属于基础题．
练习册系列答案
相关题目
9．如图是函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜2π）在一个周期内的图象，则（ ）
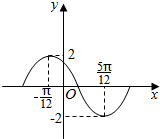
| A． | A=2，ω=2，φ=$\frac{π}{3}$ | B． | A=2，ω=2，φ=$\frac{2π}{3}$ | C． | A=2，ω=$\frac{1}{2}$，φ=-$\frac{π}{3}$ | D． | A=2，ω=2，φ=-$\frac{π}{3}$ |
6．在一次模拟考试后，从高三某班随机抽取了20位学生的数学成绩，其分布如下：
分数在130分（包括130分）以上者为优秀，据此估计该班的优秀率约为（ ）
| 分组 | [90，100] | [100，110） | [110，120） | [120，130） | [130，140） | [140，150） |
| 频数 | 1 | 2 | 6 | 7 | 3 | 1 |
| A． | 10% | B． | 20% | C． | 30% | D． | 40% |
有一个容量为n的样本，其频率分布直方图如图所示，已知样本数据在区间[10，12）内的频数为18，则实数n=100．
10．某校羽毛球小组有男学生A，B，C和女学生X，Y，Z共6人，其所属年级如下：
现从这6名学生中随机选出2人参加羽毛球比赛（每人被选到的可能性相同）．
（1）共有几种不同的选法？用表中字母列举出来；
（2）设M为事件“选出的2人性别相同”，求事件M发生的概率．
| 一年级 | 二年级 | 三年级 | |
| 男生 | A | B | C |
| 女生 | X | Y | Z |
（1）共有几种不同的选法？用表中字母列举出来；
（2）设M为事件“选出的2人性别相同”，求事件M发生的概率．
7．已知幂函数y=f（x），f（8）=2$\sqrt{2}$，则y=f（x）一定经过的点是（ ）
| A． | （2，1） | B． | （2，4） | C． | （4，2） | D． | （0，1） |