关于函数f(x)=x2-2x+1的零点.下列说法正确的是( )A．因为f在(0.2)内没有零点B．因为1是f?f(2)＜0C．由于f上单调递减.所以f内有唯一的一个零点D．以上说法都不对题目和参考答案——青夏教育精英家教网—

题目内容

13．关于函数f（x）=x²-2x+1的零点，下列说法正确的是（　　）

	A．	因为f（0）?f（2）＞0，所以f（x）在（0，2）内没有零点
	B．	因为1是f（x）的一个零点，所以f（0）?f（2）＜0
	C．	由于f（x）在区间（-∞，0）上单调递减，所以f（x）在（-∞，0）内有唯一的一个零点
	D．	以上说法都不对

分析求得f（x）的零点为1，可判断A；由f（x）在（0，2）不单调，可判断B；由图象在（-∞，0）内可能与x轴没有交点，可判断C，进而得到结论．

解答解：函数f（x）=x²-2x+1的零点，
即为f（x）=（x-1）²=0，解得x=1，即零点为1．
对A，因为f（0）•f（2）＞0，所以f（x）在（0，2）内没有零点，
错误，还要考虑（0，2）内的某个函数值的符号，比如f（1）=0；
对B，因为1是f（x）的一个零点，所以f（0）•f（2）＜0，
错误，要考虑（0，2）的单调性，事实上，f（0）•f（2）＞0；
对C，由于f（x）在区间（-∞，0）上单调递减，
所以f（x）在（-∞，0）内有唯一的一个零点．
错误，图象在（-∞，0）内与x轴没有交点．
故选：D．

点评本题考查函数的零点问题，以及函数零点定理的运用，注意结合图象与x轴的关系，考查判断能力，属于基础题．

练习册系列答案

4．若偶函数y=f（x）（x∈R）满足f（1+x）=f（1-x），且当x∈[-1，0]时，f（x）=x²，则函数g（x）=f（x）-|lgx|的零点个数为10个．

1．

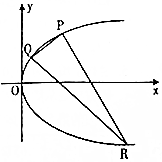已知抛物线C：y²=4x，P为C上一点且纵坐标为2，Q，R是C上的两个动点，且PQ⊥PR．
（Ⅰ）求过点P，且与C恰有一个公共点的直线l的方程；
（Ⅱ）求证：QP过定点，并求出定点坐标．

8．

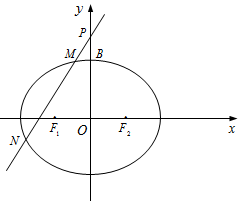已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左，右焦点分别为F₁，F₂，上顶点为B．Q为抛物线y²=24x的焦点，且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$，$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过定点P（0，4）的直线l与椭圆C交于M，N两点（M在P，N之间），设直线l的斜率为k（k＞0），在x轴上是否存在点A（m，0），使得以AM，AN为邻边的平行四边形为菱形？若存在，求出实数m的取值范围；若不存在，请说明理由．

18．如果点P（sin2θ，2cosθ）位于第三象限，那么角θ所在的象限是（　　）

5．（1）已知y=sinx+cosx，x∈R，求y的范围；
（2）已知y=sinx+cosx-sin2x，x∈R，求y的范围．

2．sin40°（tan190°-$\sqrt{3}$）=-1．

3．为了得到函数y=2sin（2x-$\frac{π}{3}$）的图象，只需把函数y=2sinx（2x+$\frac{π}{6}$）的图象上所有的点（　　）

	A．	向左平行平移$\frac{π}{2}$个单位长度		B．	向右平行平移$\frac{π}{4}$个单位长度
	C．	向右平行平移$\frac{π}{2}$个单位长度		D．	向左平行平移$\frac{π}{4}$个单位长度

试题分类