题目内容
8.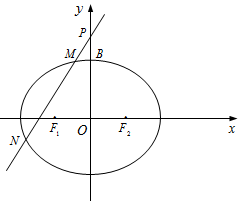 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过定点P(0,4)的直线l与椭圆C交于M,N两点(M在P,N之间),设直线l的斜率为k(k>0),在x轴上是否存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形?若存在,求出实数m的取值范围;若不存在,请说明理由.
分析 (Ⅰ)由已知Q(6,0),F1B⊥QB,|QF1|=4c=6+c,解得c=2. 在Rt△F1BQ中,|BF2|=2c=a,所以a=4,由此能求出椭圆C的标准方程.
(Ⅱ)设l:y=kx+4(k>0),M(x1,y1),N(x2,y2),取MN的中点为E(x0,y0).假设存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形,联立$\left\{\begin{array}{l}{y=kx+4}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$⇒(4k2+3)x2+32kx+16=0,由此利用韦达定理结合已知条件能求出实数m的取值范围.
解答 解:(Ⅰ)由已知Q(6,0),F1B⊥QB,
|QF1|=4c=6+c,所以c=2. …(1分)
在Rt△F1BQ中,F2为线段F1Q的中点,
故|BF2|=2c=4,所以a=4.…(2分)
于是椭圆C的标准方程为$\frac{x^2}{16}+\frac{y^2}{12}=1$.
(Ⅱ)设l:y=kx+4(k>0),M(x1,y1),N(x2,y2),取MN的中点为E(x0,y0).
假设存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形,则AE⊥MN.
联立$\left\{\begin{array}{l}{y=kx+4}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$⇒(4k2+3)x2+32kx+16=0
△>0⇒k$>\frac{1}{2}$.$\frac{-32k}{4{k}^{2}+3}$∴$\frac{-16k}{4{k}^{2}+3}$,y0=kx0+4=$\frac{12}{4{k}^{2}+3}$.
因为AE⊥MN,所以kAE=-$\frac{1}{k}$.
$\frac{12}{4{k}^{2}+3}=-\frac{1}{k}×(-\frac{16k}{4{k}^{2}+3}-m)$⇒m=-$\frac{4k}{4{k}^{2}+3}=-\frac{4}{4k+\frac{3}{k}}$.
∵$k>\frac{1}{2}$,∴$4k+\frac{3}{k}≥4\sqrt{3},\frac{1}{4k+\frac{3}{k}}∈(0,\frac{\sqrt{3}}{12}]$
所以m$∈[-\frac{\sqrt{3}}{3},0]$.
点评 本题考查椭圆C的标准方程的求法,考查在x轴上是否存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形的确定与实数m的取值范围的求法,解题时要认真审题,注意函数与方程思想的合理运用.

| 分组 | 频数 | 频率 |
| [-3,-2) | ① | 0.10 |
| [-2,-1) | 8 | 0.16 |
| (1,2] | ② | 0.50 |
| (2,3] | 10 | ③ |
| (3,4] | ④ | 0.04 |
| 合计 | 50 | 1.00 |
(2)估计该厂生产的此种产品中,不合格的直径长与标准值的差落在(1,3]内的概率;
(3)现对该厂这种产品的某批次进行检查,结果发现有20件产品不合格,据此估算这批产品中合格品的件数.
| A. | {x|-1≤x≤2} | B. | {x|-1<x≤2} | C. | {x|-1<x≤0} | D. | {x|-1<x≤3} |
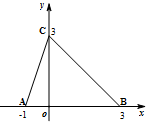
| A. | 因为f(0)?f(2)>0,所以f(x)在(0,2)内没有零点 | |
| B. | 因为1是f(x)的一个零点,所以f(0)?f(2)<0 | |
| C. | 由于f(x)在区间(-∞,0)上单调递减,所以f(x)在(-∞,0)内有唯一的一个零点 | |
| D. | 以上说法都不对 |
| A. | -$\frac{33}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{63}{65}$ | D. | $\frac{63}{65}$或$\frac{33}{65}$ |
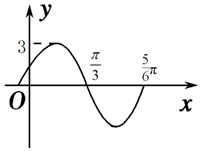 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | f(x)的一个对称中心为$(\frac{4π}{3},0)$ | B. | f(x)的图象关于直线$x=-\frac{1}{12}π$ 对称 | ||
| C. | f(x)在$[-π,-\frac{π}{2}]$上是增函数 | D. | f(x)的周期为$\frac{π}{2}$ |