题目内容
已知:函数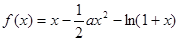 ,其中
,其中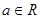 .
.
(Ⅰ)若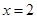 是
是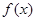 的极值点,求
的极值点,求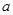 的值;
的值;
(Ⅱ)求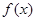 的单调区间;
的单调区间;
(Ⅲ)若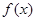 在
在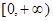 上的最大值是
上的最大值是 ,求
,求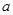 的取值范围.
的取值范围.
【答案】
(Ⅰ)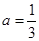
(Ⅱ)当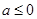 时,
时,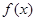 的增区间是
的增区间是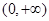 ,减区间是
,减区间是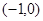 ;
;
当 时,
时,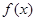 的增区间是
的增区间是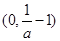 ,减区间是
,减区间是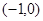 和
和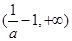 ;
;
当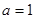 时,
时,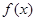 的减区间是
的减区间是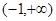 ;
;
当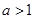 时,
时,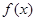 的增区间是
的增区间是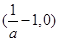 ;减区间是
;减区间是 和
和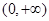 .
.
(Ⅲ)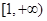
【解析】
试题分析:(Ⅰ)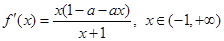 .
.
依题意,令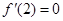 ,解得
,解得 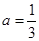 .
.
经检验,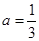 时,符合题意. ……4分
时,符合题意. ……4分
(Ⅱ)① 当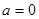 时,
时,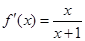 .
.
故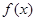 的单调增区间是
的单调增区间是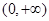 ;单调减区间是
;单调减区间是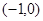 . ……5分
. ……5分
② 当 时,令
时,令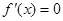 ,得
,得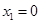 ,或
,或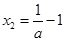 .
.
当 时,
时,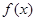 与
与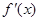 的情况如下:
的情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↘ |
|
↗ |
|
↘ |
所以,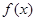 的单调增区间是
的单调增区间是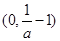 ;单调减区间是
;单调减区间是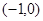 和
和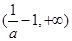 .
.
当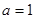 时,
时,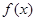 的单调减区间是
的单调减区间是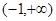 .
.
当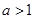 时,
时,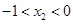 ,
,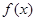 与
与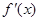 的情况如下:
的情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↘ |
|
↗ |
|
↘ |
所以,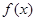 的单调增区间是
的单调增区间是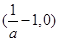 ;单调减区间是
;单调减区间是 和
和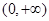 .
.
③ 当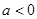 时,
时,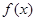 的单调增区间是
的单调增区间是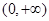 ;单调减区间是
;单调减区间是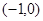 .
.
综上,当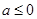 时,
时,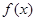 的增区间是
的增区间是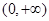 ,减区间是
,减区间是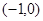 ;
;
当 时,
时,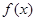 的增区间是
的增区间是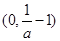 ,减区间是
,减区间是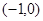 和
和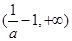 ;
;
当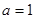 时,
时,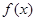 的减区间是
的减区间是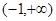 ;
;
当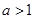 时,
时,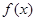 的增区间是
的增区间是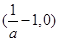 ;减区间是
;减区间是 和
和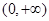 . ……11分
. ……11分
(Ⅲ)由(Ⅱ)知 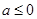 时,
时,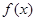 在
在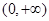 上单调递增,
上单调递增,
由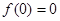 ,知不合题意.
,知不合题意.
当 时,
时,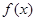 在
在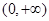 的最大值是
的最大值是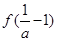 ,
,
由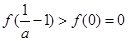 ,知不合题意.
,知不合题意.
当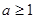 时,
时,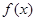 在
在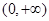 单调递减,
单调递减,
可得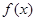 在
在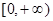 上的最大值是
上的最大值是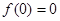 ,符合题意.
,符合题意.
所以,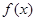 在
在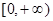 上的最大值是
上的最大值是 时,
时,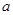 的取值范围是
的取值范围是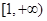 . ……14分
. ……14分
考点:本小题主要考查函数极值的应用、利用导数求函数的单调性和已知最值求参数的取值范围,考查学生分类讨论思想的应用和逻辑推理能力.
点评:用导数求函数的单调区间时最好画出表格,这样既清楚又简单,另外分类讨论时要尽量做到不重不漏.

练习册系列答案
相关题目
















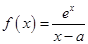 (其中常数
(其中常数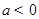 ).
).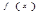 的单调区间;
的单调区间; ,使得不等式
,使得不等式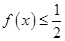 成立,求a的取值范围.
成立,求a的取值范围.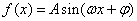 (其中
(其中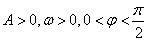 )的
)的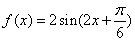 图象与
图象与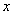 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为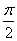 ,且图象上一个最低点为
,且图象上一个最低点为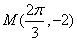 。
。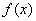 的解析式; (2)当
的解析式; (2)当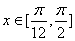 ,求:函数
,求:函数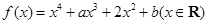 ,其中
,其中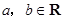 .
.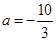 时,讨论函数
时,讨论函数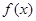 的单调性;
的单调性;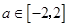 ,不等式
,不等式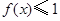 在
在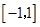 上恒成立,求
上恒成立,求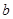 的取值范围.
的取值范围.