题目内容
在平面直角坐标系xOy中,焦点为(-2,0)的抛物线的标准方程为 .
考点:抛物线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设出抛物线的标准方程,根据焦点坐标求出p的值,代入可得到答案.
解答:
解:设抛物线的标准方程为y2=-2px(p>0),则
因为焦点为F(-2,0),
所以
=2,
所以p=4,
所以抛物线C的标准方程为y2=-8x.
故答案为:y2=-8x.
因为焦点为F(-2,0),
所以
| p |
| 2 |
所以p=4,
所以抛物线C的标准方程为y2=-8x.
故答案为:y2=-8x.
点评:本题主要考查抛物线的标准方程,定位定量是关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
若α、β都是锐角,且sinα=
,cos(α+β)=-
,则sinβ的值是( )
| 5 |
| 13 |
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
过点M(1,2)的直线l与圆C:(x-3)2+( y-4)2=25交于A、B两点,C为圆心,当∠ACB最小时,直线l的方程是( )
| A、x-2y+3=0 |
| B、2x+y-4=0 |
| C、x-y+1=0 |
| D、x+y-3=0 |
下列叙述中正确的是( )
| A、若 p∧(¬q)为假,则一定是p假q真 |
| B、命题“?x∈R,x2≥0”的否定是“?x∈R,x2≥0” |
| C、若a,b,c∈R,则“ab2>cb2”的充分不必要条件是“a>c” |
| D、设α是一平面,a,b是两条不同的直线,若 a⊥α,b⊥α,则a∥b |
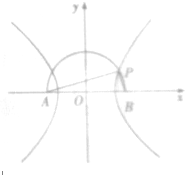 如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是
如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是