题目内容

参数方程
x=t+
1
t
y=t-
1
t
表示的曲线是（　　）
A、椭圆B、双曲线C、抛物线D、圆
考点：参数方程化成普通方程
专题：坐标系和参数方程
分析：把参数方程
x=t+
1
t
y=t-
1
t
（t为参数）消去参数，化为普通方程后，即可得到结论．
解答： 解：参数方程
x=t+
1
t
…①
y=t-
1
t
…②
，
①2-②2可得：x2-y2=4．
参数方程
x=t+
1
t
y=t-
1
t
表示的曲线是双曲线．
故选：B．
点评：本题考查参数方程与普通方程之间的转化，关键是利用已知条件消去参数．
练习册系列答案
相关题目
已知矩形ABCD，AB=6，BC=8，则以A，B为焦点且过C，D点的椭圆的标准方程为
 
．
函数y=2sin（
π
2
-2x），x∈[0，π]为增函数的区间是（　　）
A、[0，
π
3
]
B、[
π
12
，
7
12
]
C、[
π
2
，
5π
6
]
D、[
π
6
，π]
在区间[
1
2
，2]上，函数f（x）=x2+bx+c（b、c∈R）与g（x）=
x2+x+1
x
在同一点取得相同的最小值，那么f（x）在区间[
1
2
，2]上的最大值是（　　）
A、
13
4
B、4
C、8
D、
5
4
设a，b是不同的直线，α，β是不同的平面，则下列结论错误的是（　　）
A、若a⊥α，b∥α，则a⊥b
B、若a⊥α，b⊥β，α∥β，则a∥b
C、若a⊥α，b∥α，b?β，则a⊥β
D、若a⊥α，a⊥β，则α∥β
函数y=f（x）是定义在实数集R上的奇函数，且当x∈（-∞，0）时，xf′（x）＜f（-x）成立，若a=
3
f（
3
），b=（lg3）f（lg3），c=（log2
1
4
）f（log2
1
4
），则a，b，c大小关系（　　）
A、c＞a＞b
B、c＞b＞a
C、a＞b＞c
D、a＞c＞b
观察下面数列的特点，选择适当的数字填入括号中．1，-4，9，-16，25，（　　），49，…
A、36B、±36
C、-36D、35
集合A={y|y=
sinx
|sinx|
+
|cosx|
cosx
}，则A的真子集有（　　）个．
A、4B、6C、7D、8
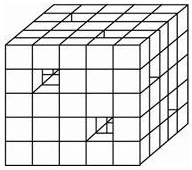如图所示，棱长为6的正方体无论从哪一个面看，都有两个直通的边长为l的正方形孔，则这个有孔正方体的表面积（含孔内各面）是（　　）
A、222B、258
C、312D、324

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网