题目内容
已知矩形ABCD,AB=6,BC=8,则以A,B为焦点且过C,D点的椭圆的标准方程为 .
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由题意知焦距2c=AB=6,由BC⊥AB,且BC=8,AB=6,知AC=10,根据椭圆的定义,得2a=AC+BC=10+8=18,由此能求出出椭圆方程.
解答:
解:∵长方形ABCD的顶点A,B为椭圆的焦点,
∴焦距2c=AB=6,其中c=3,
∵BC⊥AB,且BC=8,AB=6,
∴AC=10,根据椭圆的定义,得2a=AC+BC=10+8=18,a=9,
∴b=
=
.
∴当焦点坐标在x轴时,椭圆方程为:
+
=1,
当焦点坐标在y轴时,椭圆方程为:
+
=1.
故答案为:
+
=1或
+
=1.
∴焦距2c=AB=6,其中c=3,
∵BC⊥AB,且BC=8,AB=6,
∴AC=10,根据椭圆的定义,得2a=AC+BC=10+8=18,a=9,
∴b=
| 81-9 |
| 72 |
∴当焦点坐标在x轴时,椭圆方程为:
| x2 |
| 81 |
| y2 |
| 72 |
当焦点坐标在y轴时,椭圆方程为:
| x2 |
| 72 |
| y2 |
| 81 |
故答案为:
| x2 |
| 81 |
| y2 |
| 72 |
| x2 |
| 72 |
| y2 |
| 81 |
点评:本题考查椭圆方程的求法,是基础题,解题时要认真审题,注意椭圆性质的灵活运用.

练习册系列答案
相关题目
参数方程
表示的曲线是( )
|
| A、椭圆 | B、双曲线 | C、抛物线 | D、圆 |
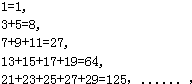
 按要求计算下列问题:
按要求计算下列问题: