题目内容
三角形ABC中，BC=7，AB=3，且
．
（Ⅰ）求AC；
（Ⅱ）求∠A．
解：（Ⅰ）由AB=3，根据正弦定理得：
（6分）
（Ⅱ）由余弦定理得：
，所以∠A=120°．（12分）
分析：（Ⅰ）由正弦定理，根据正弦值之比得到对应的边之比，把AB的值代入比例式即可求出AC的值；
（Ⅱ）利用余弦定理表示出cosA，把BC，AB及求出的AC的值代入求出cosA的值，由A为三角形的内角，利用特殊角的三角函数值即可求出A的度数．
点评：此题考查了正弦定理、余弦定理的应用，利用正弦、余弦定理可以很好得解决了三角形的边角关系，熟练掌握定理是解本题的关键．
（6分）（Ⅱ）由余弦定理得：
，所以∠A=120°．（12分）分析：（Ⅰ）由正弦定理，根据正弦值之比得到对应的边之比，把AB的值代入比例式即可求出AC的值；
（Ⅱ）利用余弦定理表示出cosA，把BC，AB及求出的AC的值代入求出cosA的值，由A为三角形的内角，利用特殊角的三角函数值即可求出A的度数．
点评：此题考查了正弦定理、余弦定理的应用，利用正弦、余弦定理可以很好得解决了三角形的边角关系，熟练掌握定理是解本题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
在三角形ABC中，BC=2，BC边上的高为
，则∠BAC的范围为（ ）
| 3 |
A、（0，
| ||
B、（0，
| ||
C、（0，
| ||
D、（0，
|
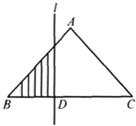如图，在等腰直角三角形ABC中，BC=4，当一条垂直于底边BC（垂足为D）的直线l从左至右移动（与直角三角形ABC有公共点）时，直线l把直角三角形分成两部分，令BD=x，试写出图中阴影部分的面积y与x的函数关系式．