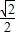题目内容
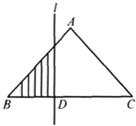 如图,在等腰直角三角形ABC中,BC=4,当一条垂直于底边BC(垂足为D)的直线l从左至右移动(与直角三角形ABC有公共点)时,直线l把直角三角形分成两部分,令BD=x,试写出图中阴影部分的面积y与x的函数关系式.
如图,在等腰直角三角形ABC中,BC=4,当一条垂直于底边BC(垂足为D)的直线l从左至右移动(与直角三角形ABC有公共点)时,直线l把直角三角形分成两部分,令BD=x,试写出图中阴影部分的面积y与x的函数关系式.分析:对边长x分类讨论,利用三角形的面积计算公式即可得出.
解答:解:当0<x≤2时,如图(1)1所示,设图中直线l与AB相交于点E,
由于△ABC是等腰直角三角形,∴DE=BD=x,
∴S△BDE=
BD•DE=
x2;
当2<x<4时,如图(2)所示,设直线l与AC相较于点E,
由于△ABC是等腰直角三角形,∴DC=DE=4-x,
∴S四边形ABDE=S△ABC-S△CDE=4-
(4-x)2=-
x2+4x-4.
∴图中阴影部分的面积y与x的函数关系式为y=
.

由于△ABC是等腰直角三角形,∴DE=BD=x,
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
当2<x<4时,如图(2)所示,设直线l与AC相较于点E,
由于△ABC是等腰直角三角形,∴DC=DE=4-x,
∴S四边形ABDE=S△ABC-S△CDE=4-
| 1 |
| 2 |
| 1 |
| 2 |
∴图中阴影部分的面积y与x的函数关系式为y=
|
点评:熟练掌握分类讨论的思想方法和直角三角形的面积计算公式等是解题的关键.

练习册系列答案
相关题目
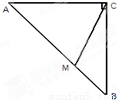
 如图,在等腰直角三角形ABC中,则AM<AC的概率为( )
如图,在等腰直角三角形ABC中,则AM<AC的概率为( )