题目内容
已知正实数x，y满足（x-1）（y+1）=16，则x+y的最小值为 ．
考点：基本不等式
专题：不等式的解法及应用
分析：变形利用基本不等式即可得出．
解答：
解：∵正实数x，y满足（x-1）（y+1）=16，
∴x=
+1，
∴x+y=
+y+1≥2
=8，当且仅当y=3，（x=5）时取等号．
∴x+y的最小值为8．
故答案为：8．
∴x=
| 16 |
| y+1 |
∴x+y=
| 16 |
| y+1 |
(y+1)•
|
∴x+y的最小值为8．
故答案为：8．
点评：本题考查了变形利用基本不等式的性质，属于基础题．
练习册系列答案
相关题目
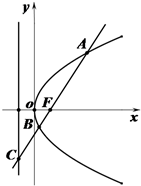如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=6，则此抛物线的方程为已知点A（-3，1，-4），B（3，-5，10）则线段AB的中点M的坐标为（ ）
| A、（0，-4，6） |
| B、（0，-2，3） |
| C、（0，2，3） |
| D、（0，-2，6） |