题目内容
从椭圆 上一点
上一点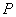 向
向 轴作垂线,垂足恰为右焦点
轴作垂线,垂足恰为右焦点 ,
,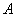 是椭圆与
是椭圆与 轴负半轴的交点,
轴负半轴的交点, 是椭圆与
是椭圆与 轴正半轴的交点,且
轴正半轴的交点,且 (
( 是坐标原点),则该椭圆的离心率是
是坐标原点),则该椭圆的离心率是
A. B.
B. C.
C. D.
D. 
D

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
题目内容
从椭圆 上一点
上一点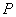 向
向 轴作垂线,垂足恰为右焦点
轴作垂线,垂足恰为右焦点 ,
,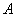 是椭圆与
是椭圆与 轴负半轴的交点,
轴负半轴的交点, 是椭圆与
是椭圆与 轴正半轴的交点,且
轴正半轴的交点,且 (
( 是坐标原点),则该椭圆的离心率是
是坐标原点),则该椭圆的离心率是
A. B.
B. C.
C. D.
D. 
D

 轻松课堂标准练系列答案
轻松课堂标准练系列答案